e-koreatech.or.kr에서의 강의 정리내용입니다.
https://e-koreatech.step.or.kr/page/lms/learning?m1=class%25&course_id=236032%25
e-koreatech
e-koreatech.step.or.kr
1회차 - 해석 준비 단계
유한요소법
- 우리 주변의 물건, 제품 등의 안전에 대해 예측해보는 것.
학습목표
- 고체역학 용어에 대해 설명할 수 있다.
- 응력/변형률의 관계와 유한요소해석의 종류에 대해 설명할 수 있다.
- 해석 대상 모델 파일 형식과 Mesh의 정의와 종류에 대해 설명할 수 있다.
학습내용
- 고체역학 묭어의 정리
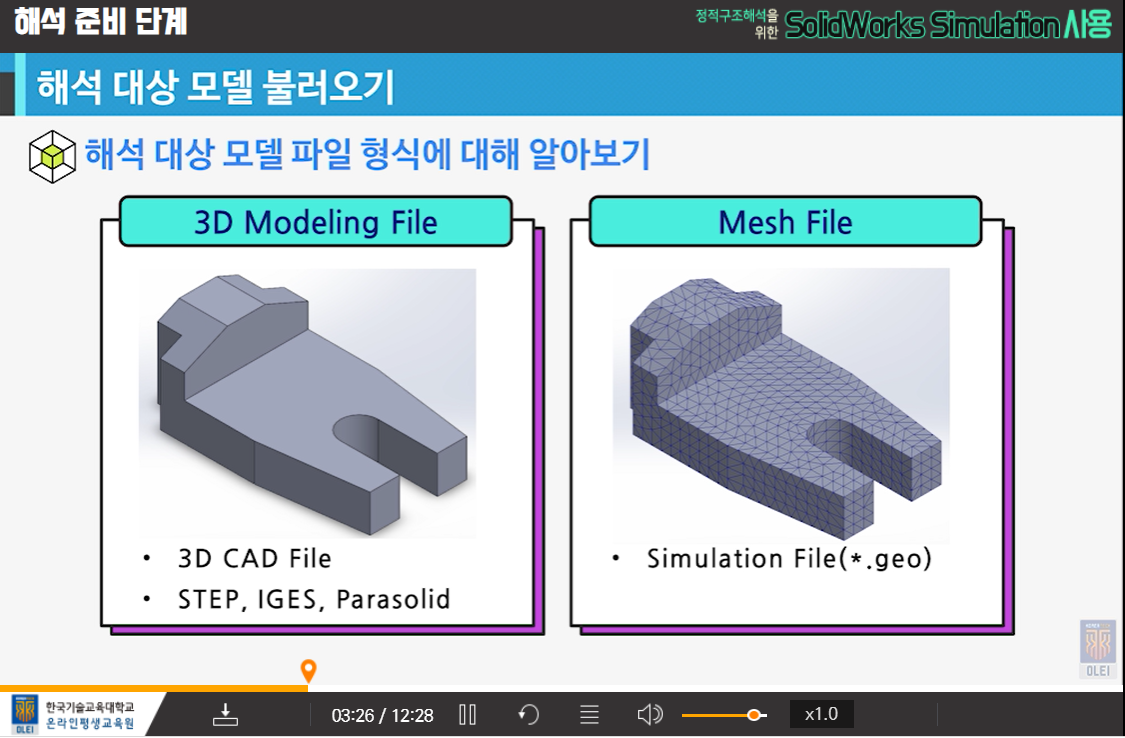
- 해석대상 모델 불러오기
응력(Stress)
- 단위 면적에 작용하는 하중
- 물체가 받는 외력의 정도
탄성영역(Elastic Zone)
- 외력을 제거했을때 원래 상태로 돌아가는 영역
소성영역(Plastic Zone)
- 외력을 제거했을 때 변형된 상태로 남아 있는 영력
탄성계수(Elastic Modulus)
- 응력/변형률 선도의 탄성영역에서 직선의 기울기
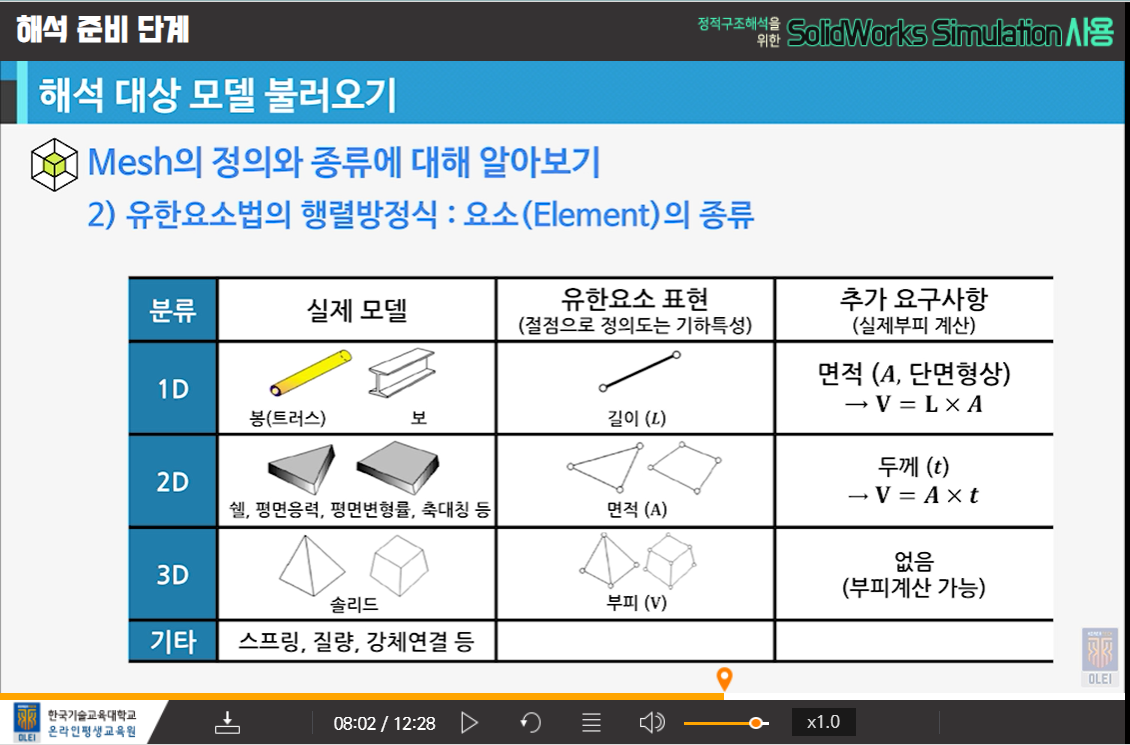
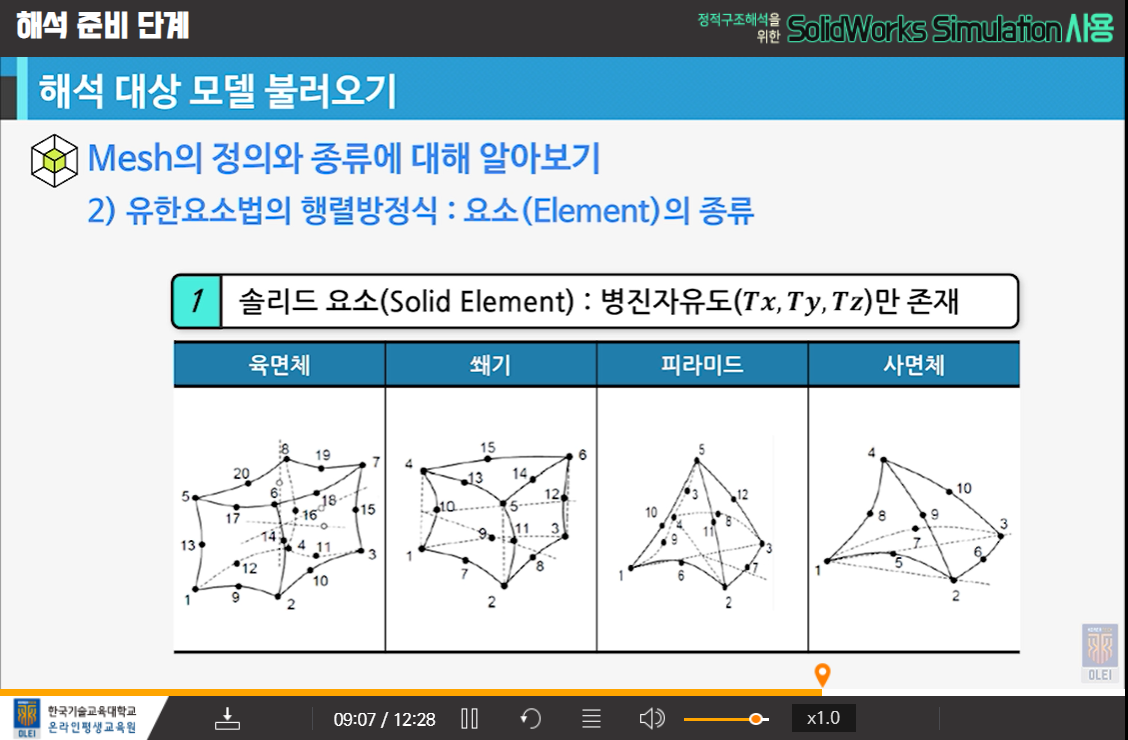
솔리드요소(Solid Element)
- 병진자유도(Tx, Ty, Tz)만 갖는 3개의 자유도를 가진다.
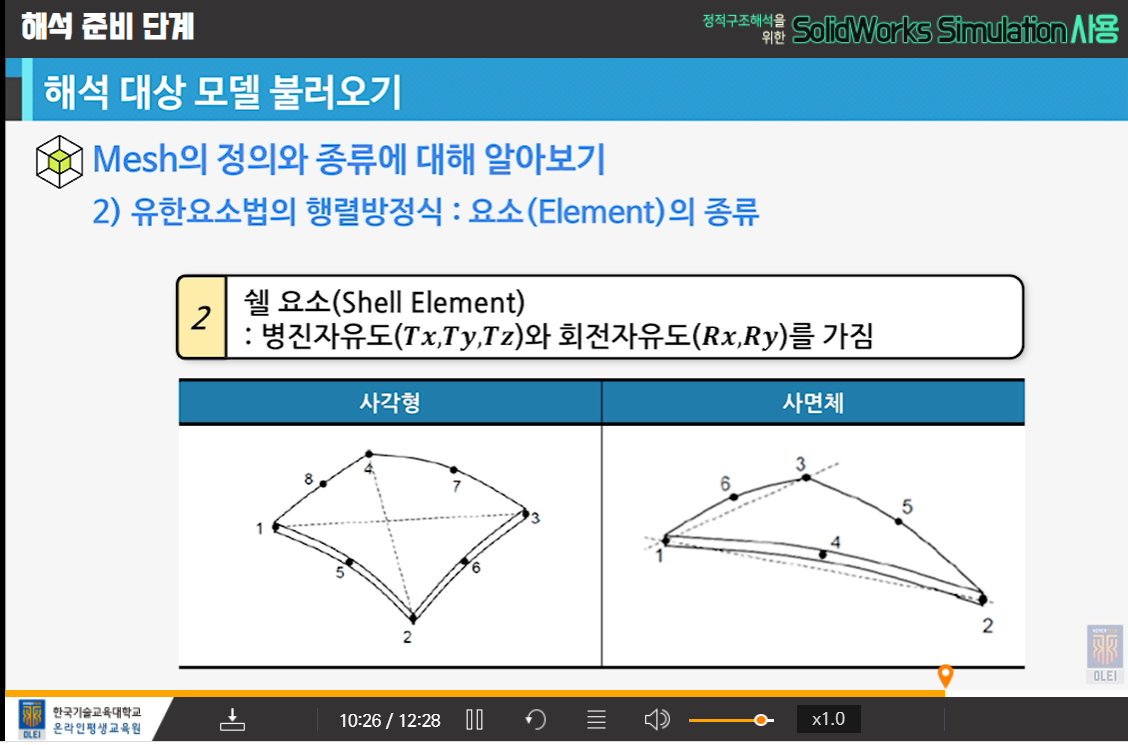
쉘요소(Shell Element)
- 병진자유도(Tx, Ty, Tz)와 회전자유도(Rx, Ry)로 5개의 자유도를 가진다.
빔요소(Beam Element)
- 병진자유도(Tx, Ty, Tz)와 회전자유도(Rx, Ry)로 5개의 자유도를 가진다.
고체역학 용어
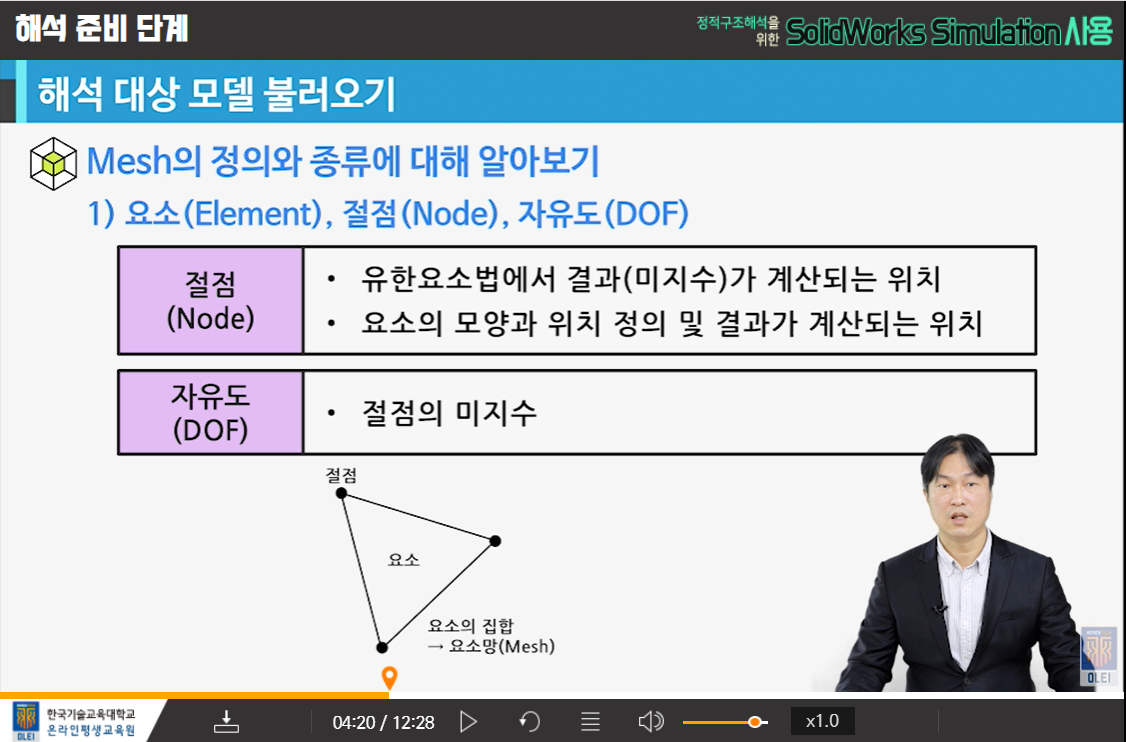
1) 변위(Displacement)
- 외부 하중 P에 의해 재료의 변형된 량으로 벡터이며, 단위는 길이(mm)이다.

2) 변형률(Strain : e)
- 변형을 측정하는 기준
- 단위는 무차원 수

3) 응력(Stress : 시그마)
- 외부 작용(하중)에 대해 물체가 모양을 유지하는데 요구되는 힘이나 애부 저항력으로 정의
- 단위는 Pa(N/m^2)

응력-변형률의 관계
1) 탄성영역(Elastic Zone)
- 작용된 하중이 제거 되었을 때 원래 상태로 되돌아가는 영역

2) 소성영역(Plasteic Zone)
- 작용된 하중이 제거 되었을 때 변형된 상태로 남아 있는 영역
3) 항복점(Yield Point)
- 소성변형이 발생하는 응력의 시작점
4) 탄성계수(Elastic Modulus)와 응력-변형률의 관계
- 탄성영역에서 응력과 변형률은 선형(직선)의 비례관계
- 직선의 기울기 = 탄성계수(Elastic Modulus ; E)

5) 후크의 법칙(Hook's Law)
- 탄성영역에서 변형률은 응력의 크기에 비례함.
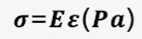
선형해석
- 구조해석
- 유동해석
- 진동소음해석
- 최적화해석
- 전자기장해석
- 열해석
- 피로해석
- 동역학해석
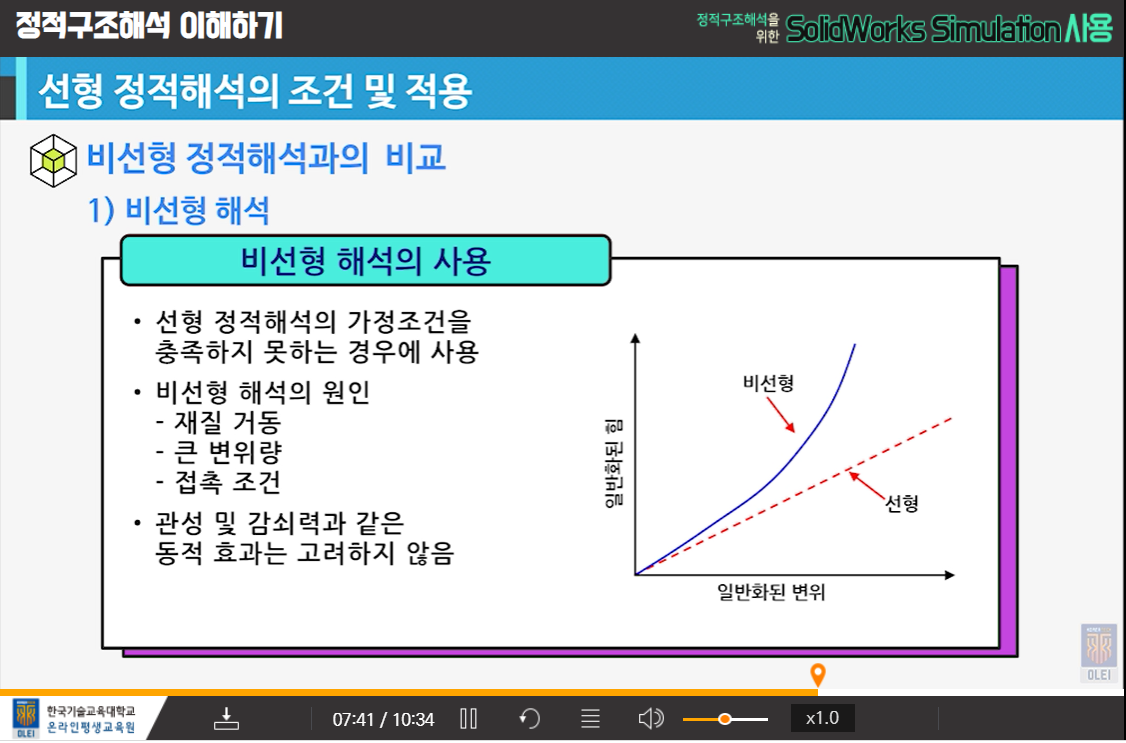
비선형해석
유한요소해석의 종류
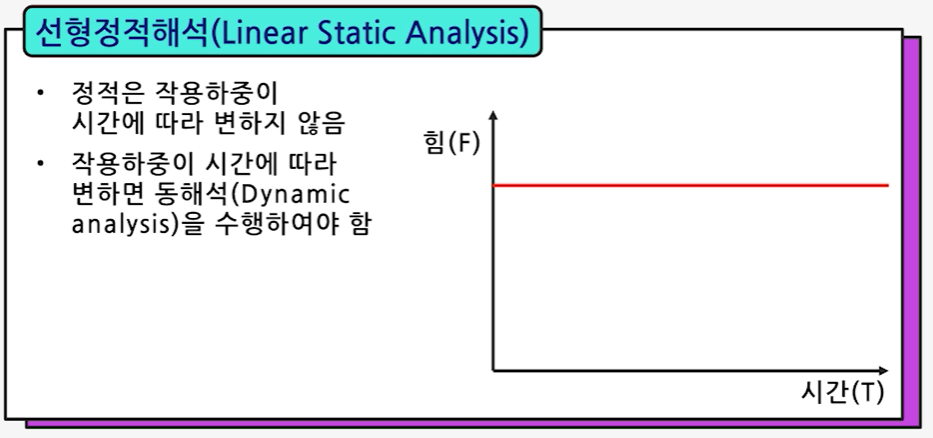
1) 선형정적해석(Linear Static Analysis)
- 정적은 작용하중이 시간에 따라 변하지 않음.
- 작용하중이 시간에 따라 변하면 동해석(Dynamic Analysis)을 수행하여야 한다.
선형해석(Linear Static Analysis)의 세가지 조건
1) 재료가 탄성영역 내에서 후크의 법칙을 따라 거동함.
- 하중과 변위, 응력과 변형률은 선혀의 관계를 가져야 함.
- 후크의 법칙을 따르지 않을 경우
-> 재료의 소성영역까지 고려할 필요가 있음.
- 응력-변형률이 관계가 미소변형률 영역에서도 선형이 아니면(예:고무재료) 재료비선형(Material Nonlinear)을 고려한 해석을 수행하여야 함.
2) 발생변형에 의한 구조물의 강성변화의 변형이 작아야 함.
- 구조물의 대변형(대변위, 대회전)을 고려하여야 할 경우 기하비선형(Geometry Nonlinear)을 고려하여야 함.
(대변형 : 예상과 다르게 큰 변형을 가지는 결과)
3) 하중이 작용하고, 구조물의 변형이 발생하는 동안 경계조건이 변하지 않아야 함.
- 하중이 작용하는 동안 경계조건이 변할 경우 경계비선형(Boundary Nonlinear)을 고려하여야 함.
- 대표적인 경계비선형해석 : 접촉해석(Contract Analysis)






2회차 - 하중 경계조건 정의
3회차 - 구속 대칭 경계조건 정의하기
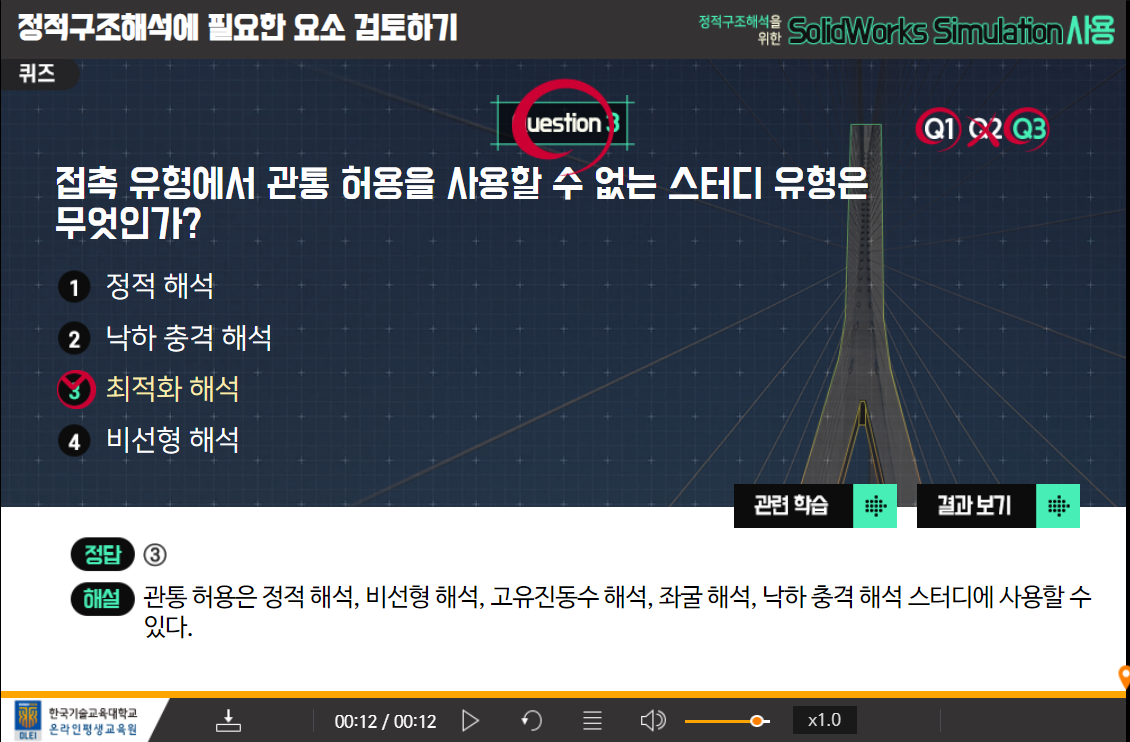
4회차 - 정적구조해석에 필요한 요소 검토하기
학습목표
- 전체 모델 해석과 대칭 모델해석에 대해 설명할 수 있다.
- 조립품에서의 단품(part) 정적구조해석에 대해 설명할 수 있다.
- 조립품에서의 접촉조건에 대해 설명할 수 있다.
학습내용
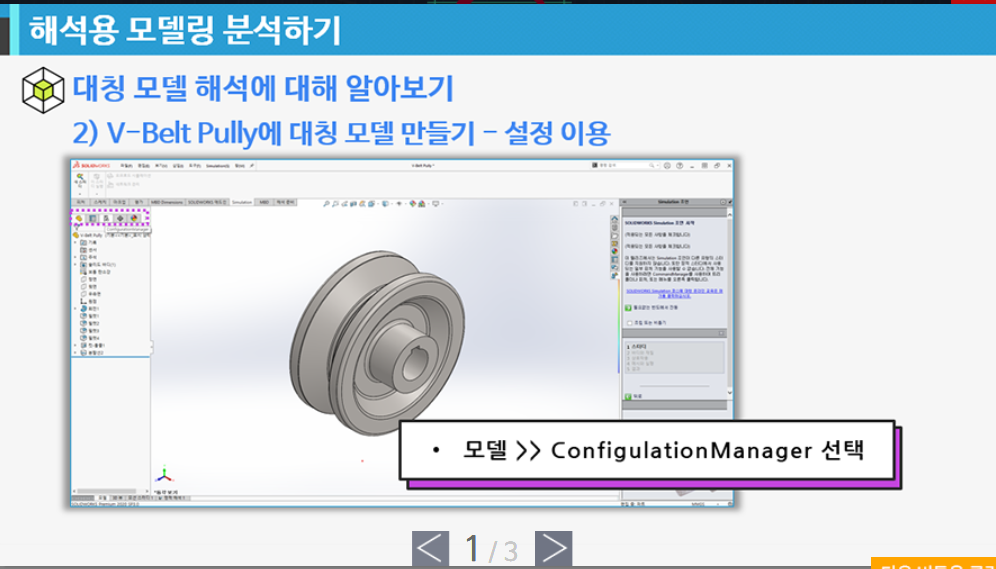
- 해석용 모델링 분석하기
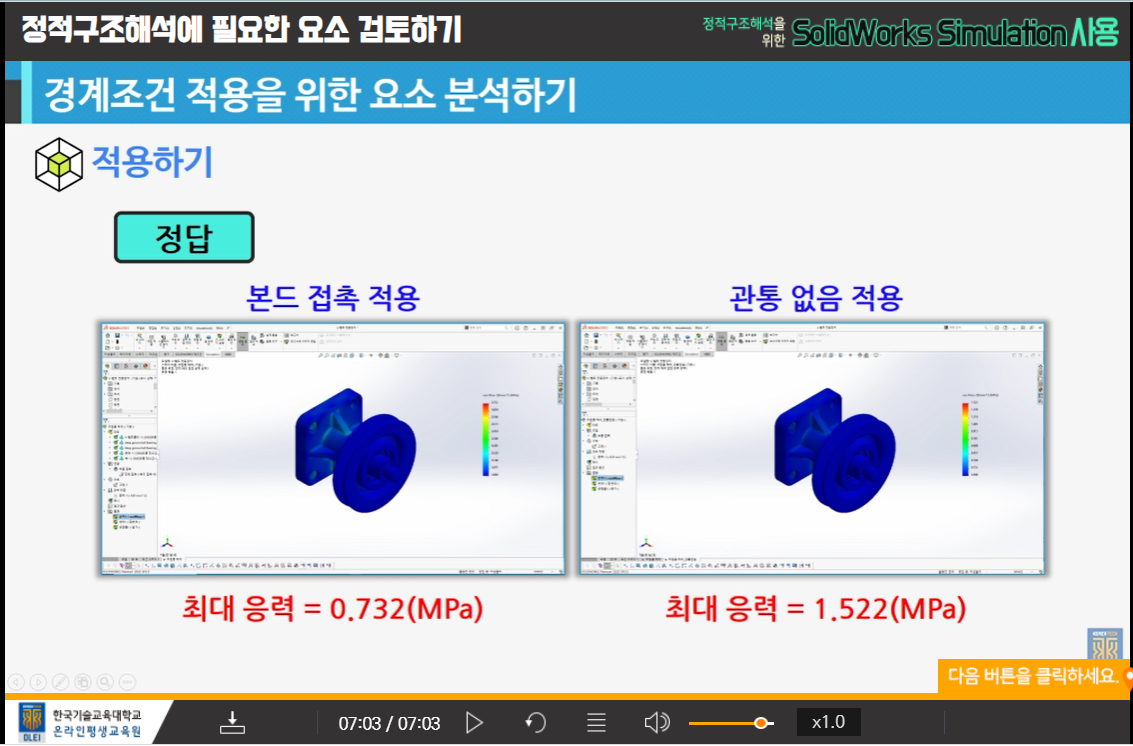
- 경계조건 적용을 위한 요소 분석하기
e-koreatech
e-koreatech.step.or.kr
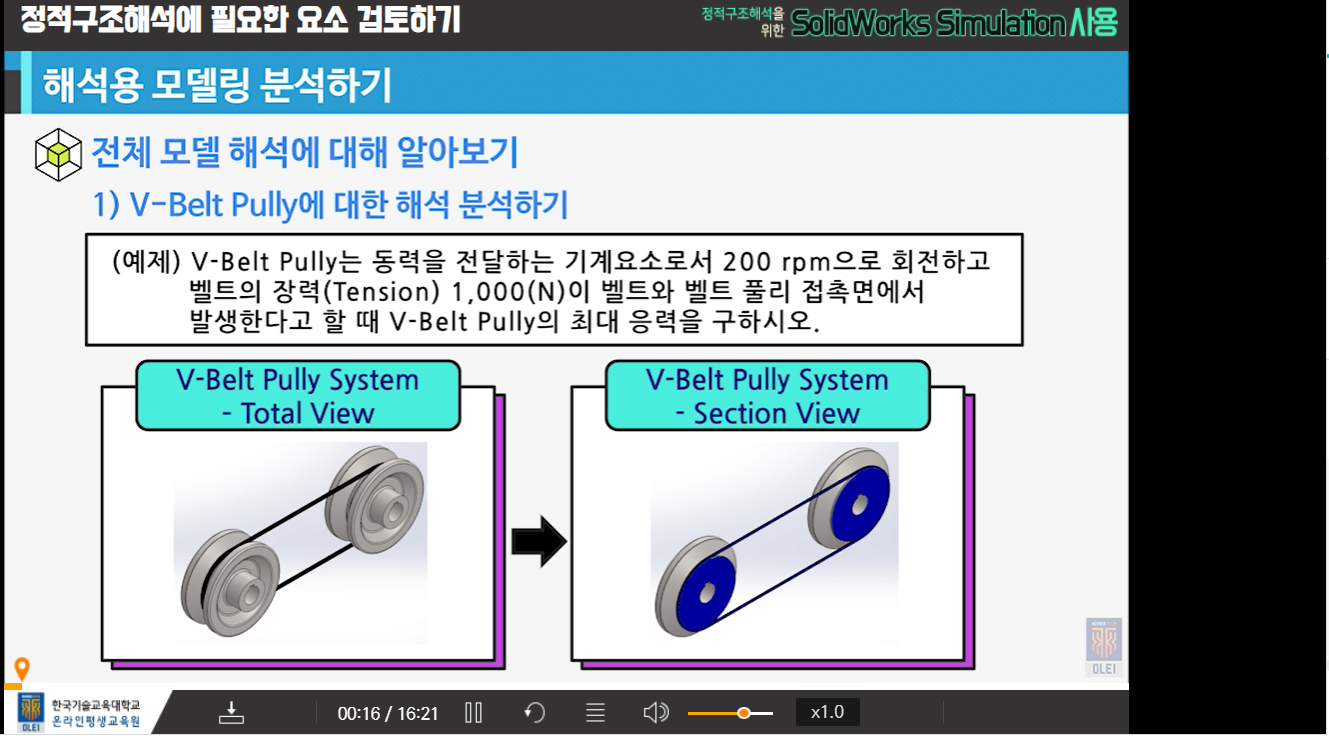
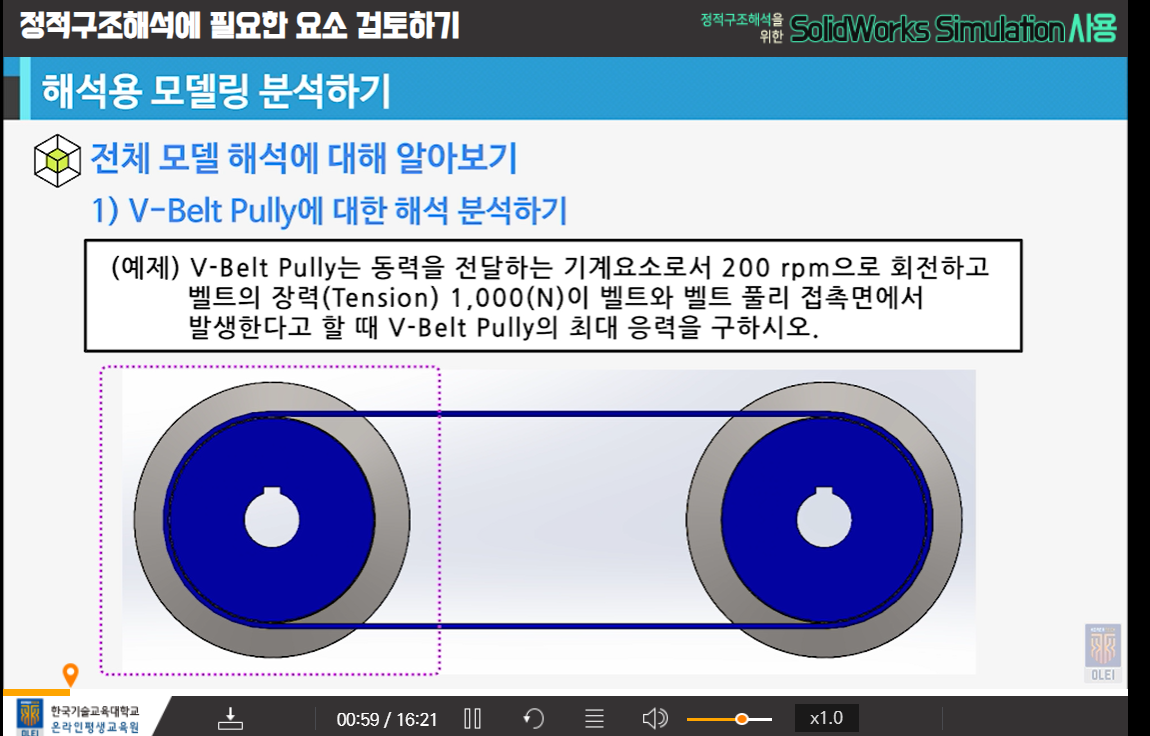

4-2 경계조건 적용을 위한 요소 분석하기
학습목표
- 조립품에서의 단품(part) 정적구조해석에 대해 설명할 수 있다.
- 조립품에서의 접촉조건에 대해 설명할 수 있다.
학습내용
- 조립품에서의 단품(part) 정적구조해석 알아보기
- 조립품에서의 접촉조건에 대해 알아보기
e-koreatech
e-koreatech.step.or.kr
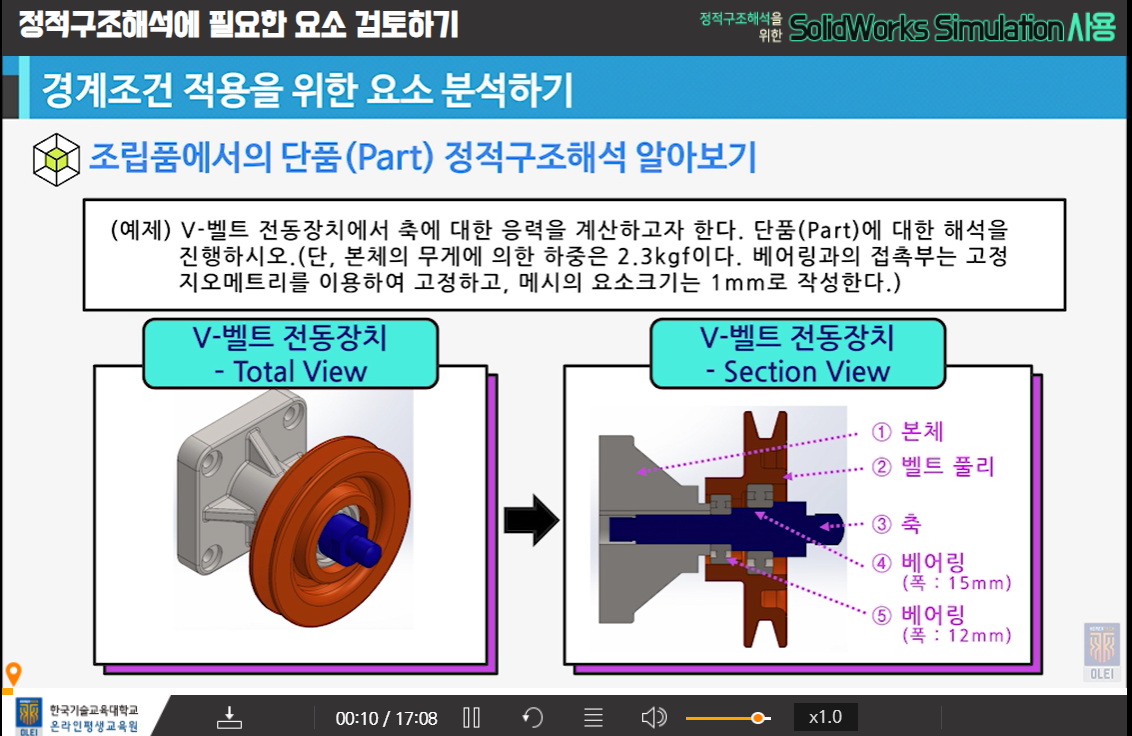



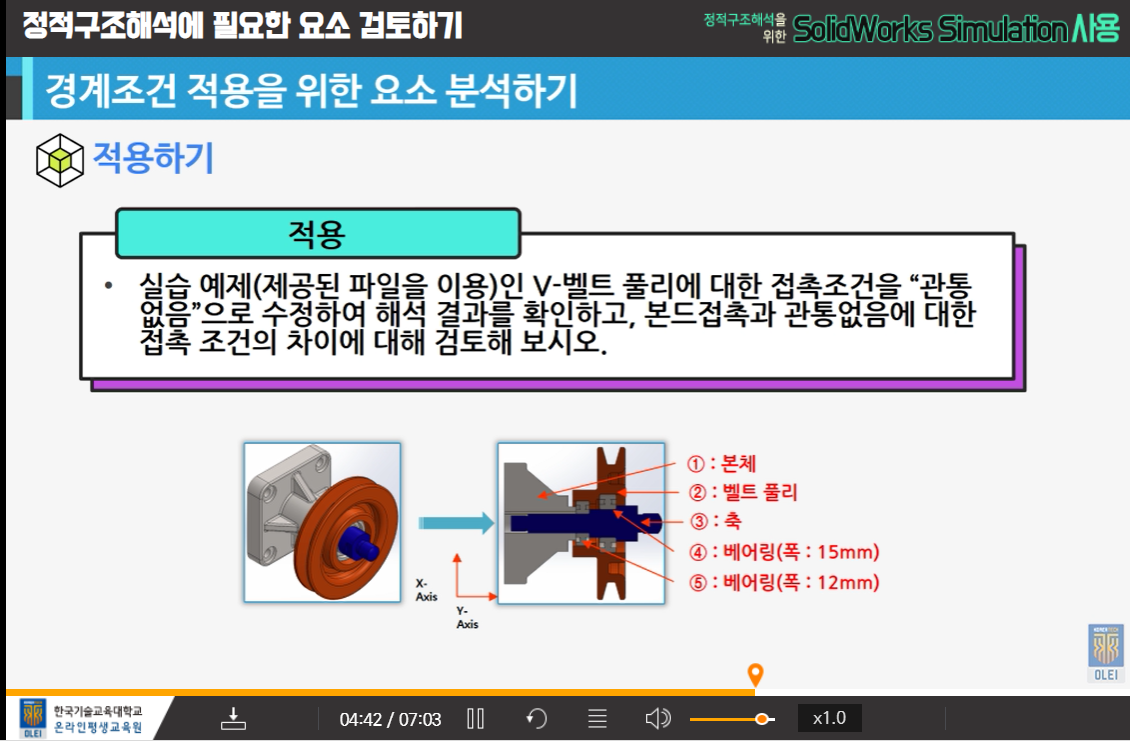
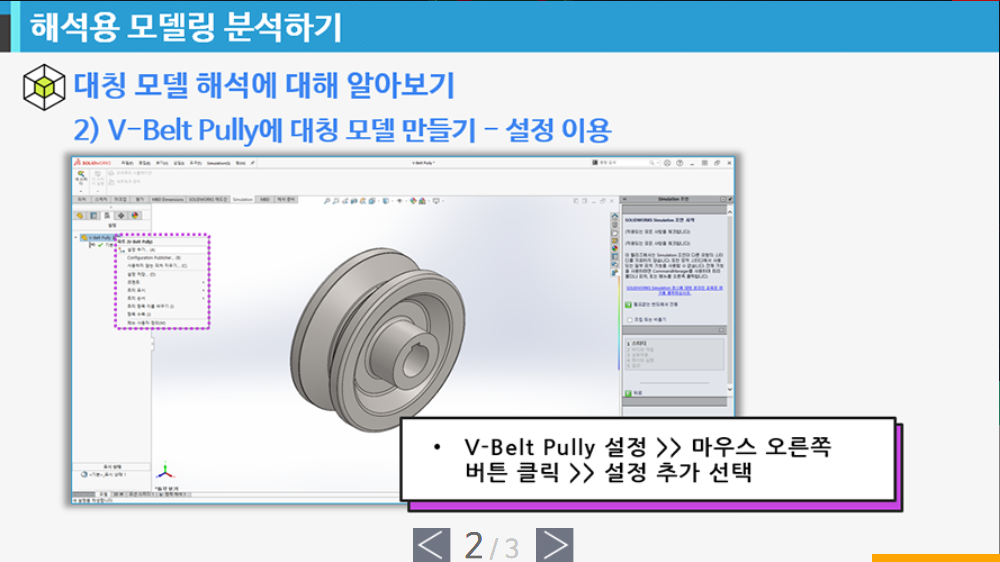
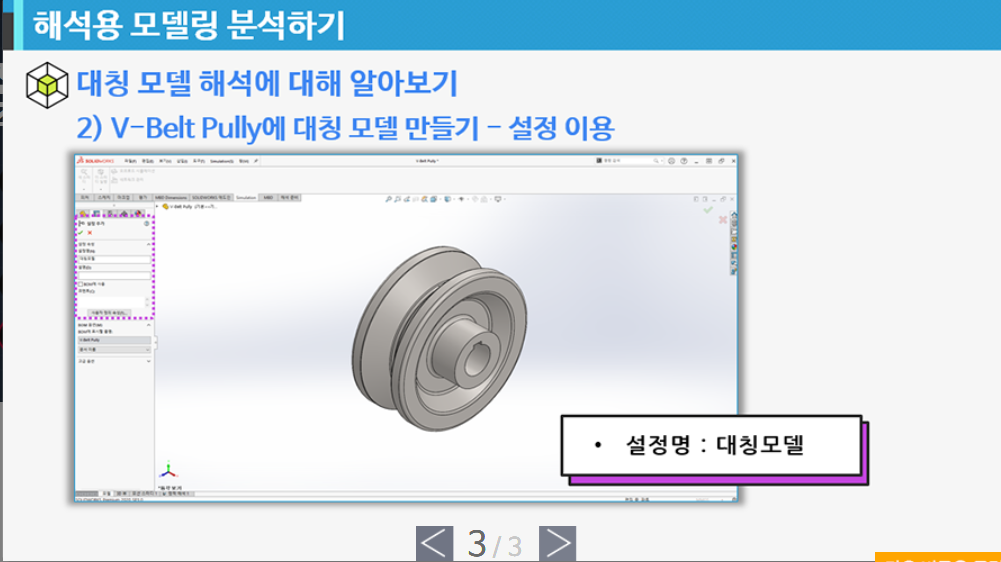

5회차 - 다중 해석조건 적용에 대해 알아보기
모니터 크기에 따른 무게 : 해석조건
받침대 : 공통으로 사용하는 조건
학습목표
- 센서의 유형을 알고, 유형별 상세 지정을 할 수 있다.
- 설계 스터디와 결과 및 그래프를 확인하고 설명할 수 있다.
- 설계 스터ㅣ 보고서 출력하기에 대해 설명할 수 있다.
학습내용
- 설계 스터디를 이용한 다중 경계조건 적용하기
- 설계 스터디에 대한 결과 확인하기
5-1 설계 스터디를 이용한 다중 경계조건 적용하기
학습목표
- 센서의 유형을 알고, 유형별 상세 지정을 할 수 있다.
학습내용
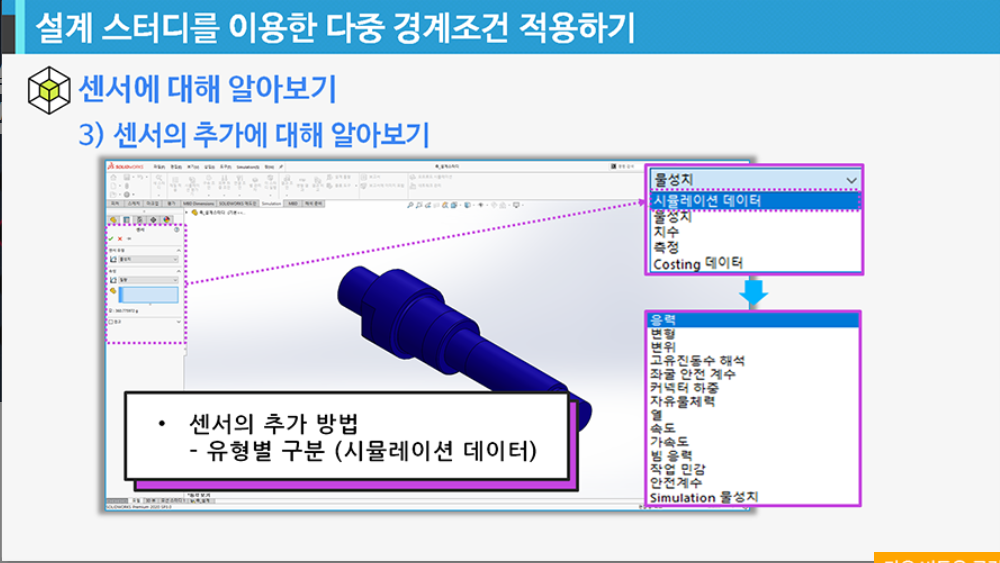
- 센서에 대해 알아보기
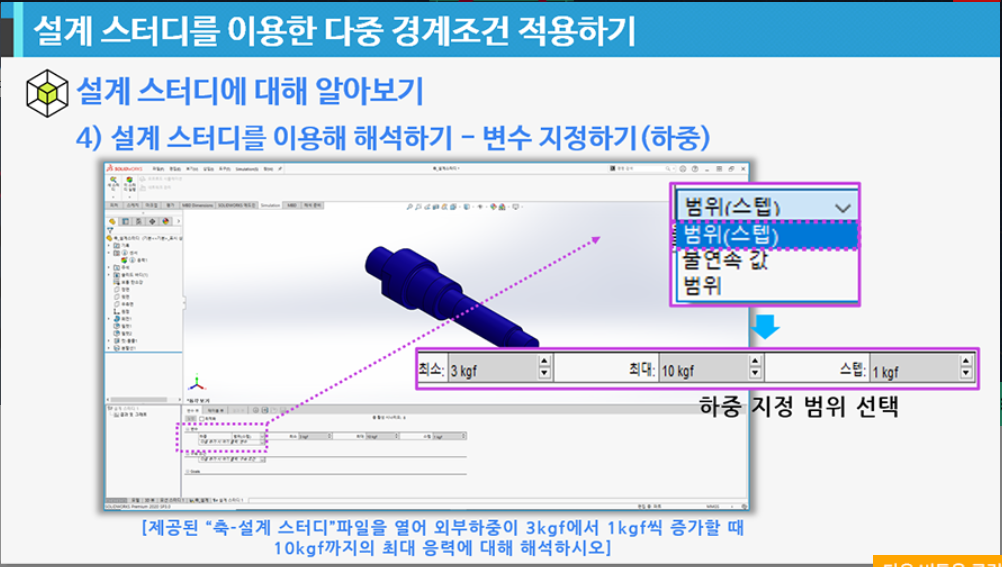
- 설계 스터디에 알아보기
5-2 설계 스터디에 대한 셜과 확인하기
학습목표
- 설계 스터디 결과 및 그래프를 확인하고 설명할 수 있다.
- 설계 스터디 보고서 출력하기에 대해 설명할 수 있다.
학습내용
- 설계 스터디 결과 및 그래프 확인하기
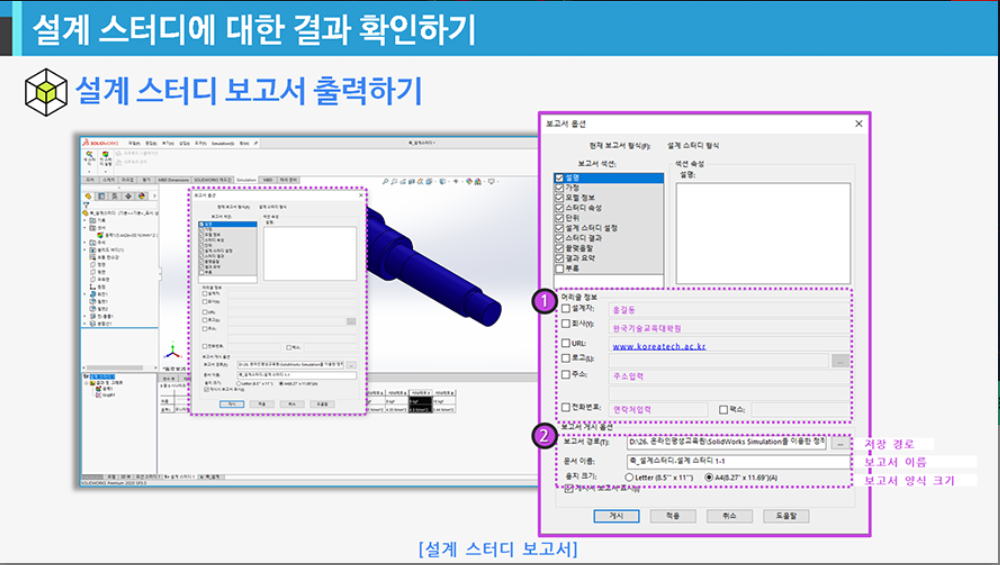
- 설계 스터디 보고서 출력하기
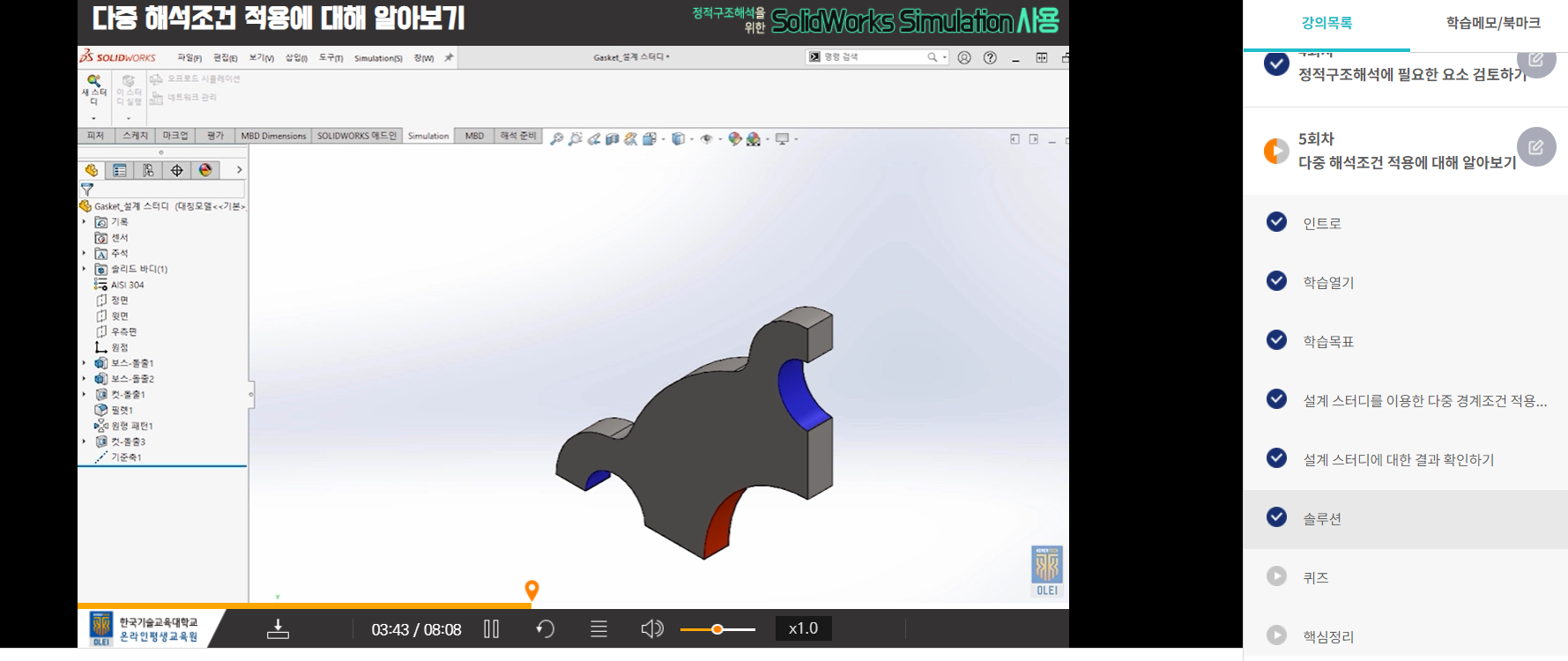
솔루션 내용 확인해보기, 2~3가지 예제가 있는데, 솔루션의 예제는 교재가 없다.

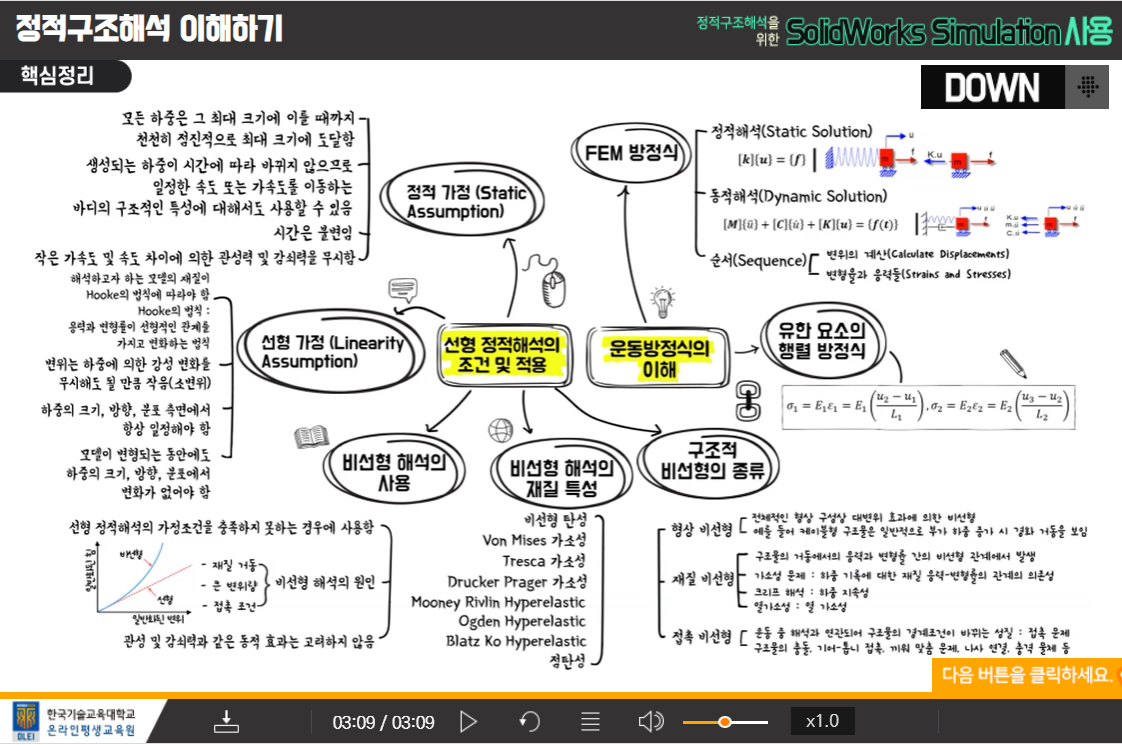
6회차 - 정적구조해석 이해하기
정적구조해석 실행을 위한 여러가지의 정의
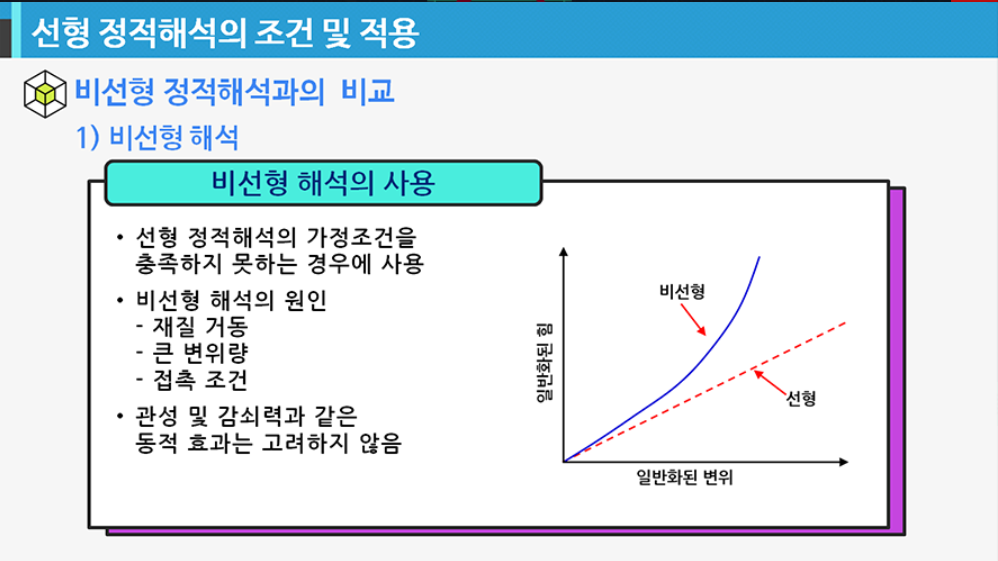
비선형 해석의 정의와 차이점
학습목표
- 강성행렬과 예제로 운동방정식에 대해 이해하고 설명할 수 있다.
- 정적해석의 가정조건에 대해 설명할 수 있다.
- 비선형해석과 비교하여 설명할 수 있다.
학습내용
6-1. 운동방정식의 이해
6-2. 선형 정적해석의 조건 및 적용
6-1. 운동방정식의 이해
학습목표
- 강성행렬에 대해 설명할 수 있다.
- 예제로 운동방정식을 이해하고 설명할 수 있다.
학습내용
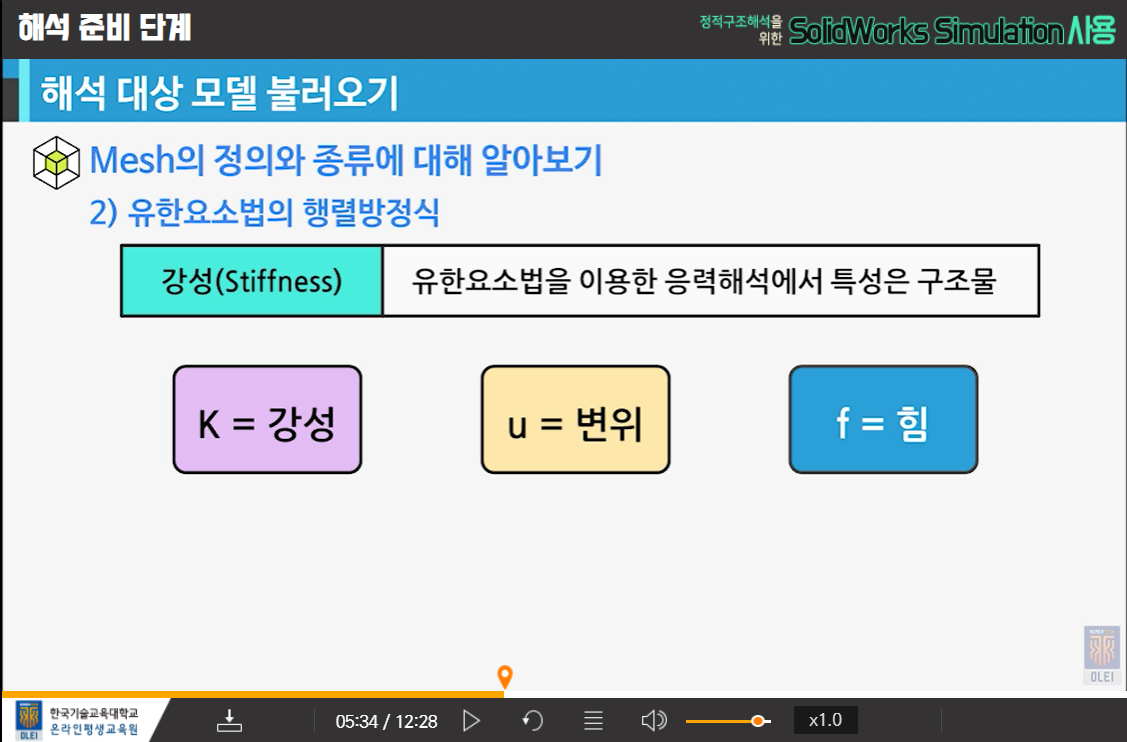
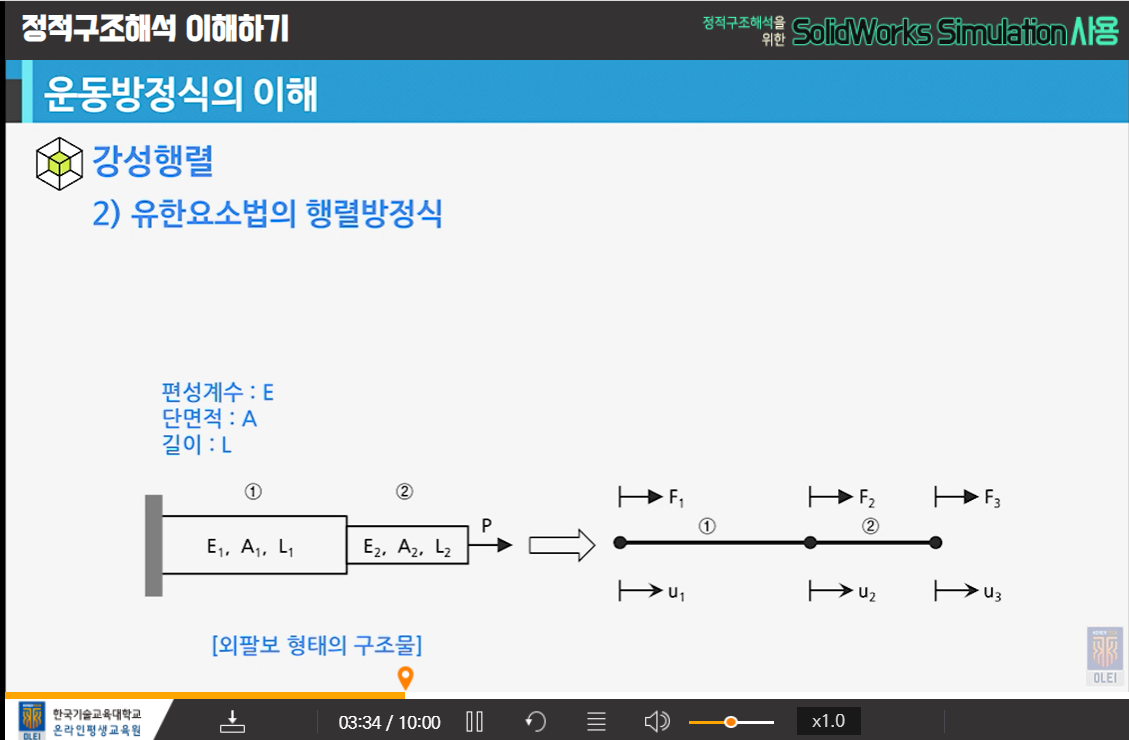
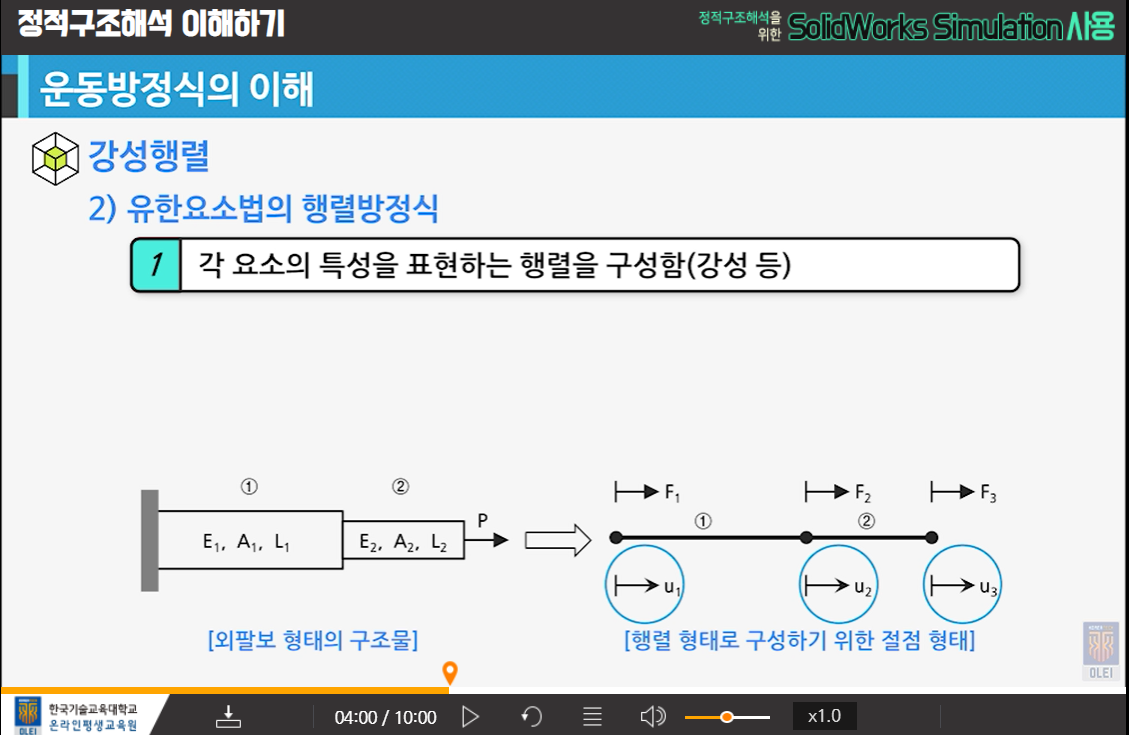
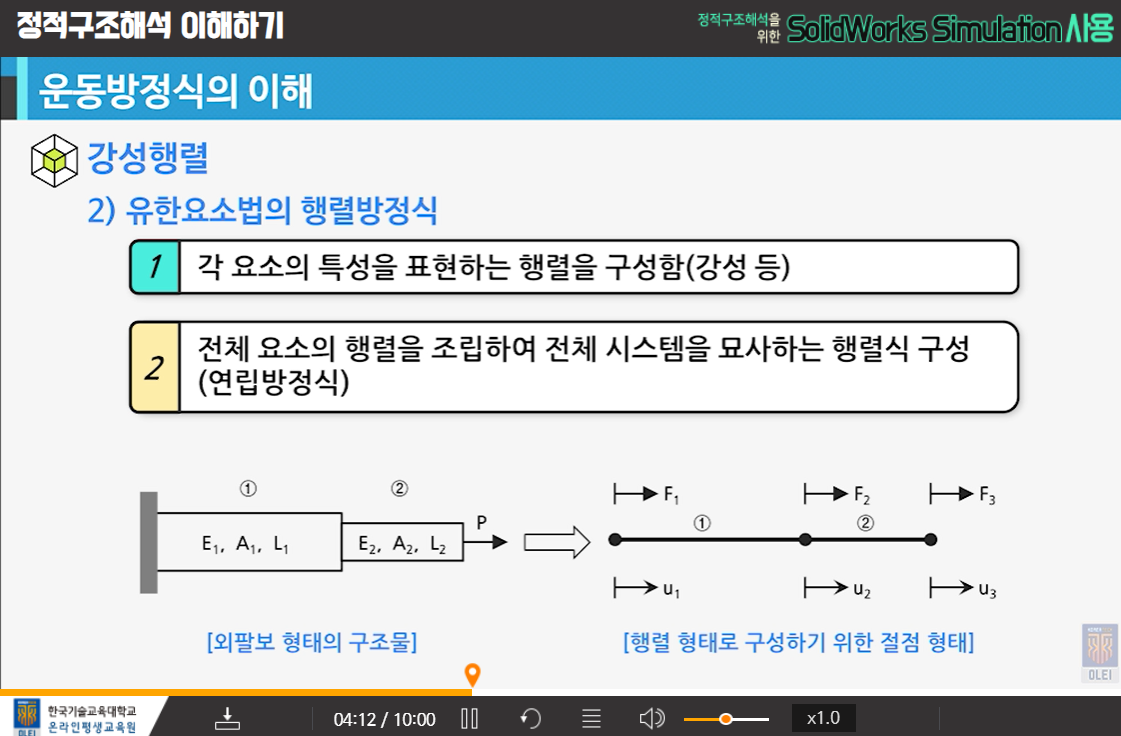
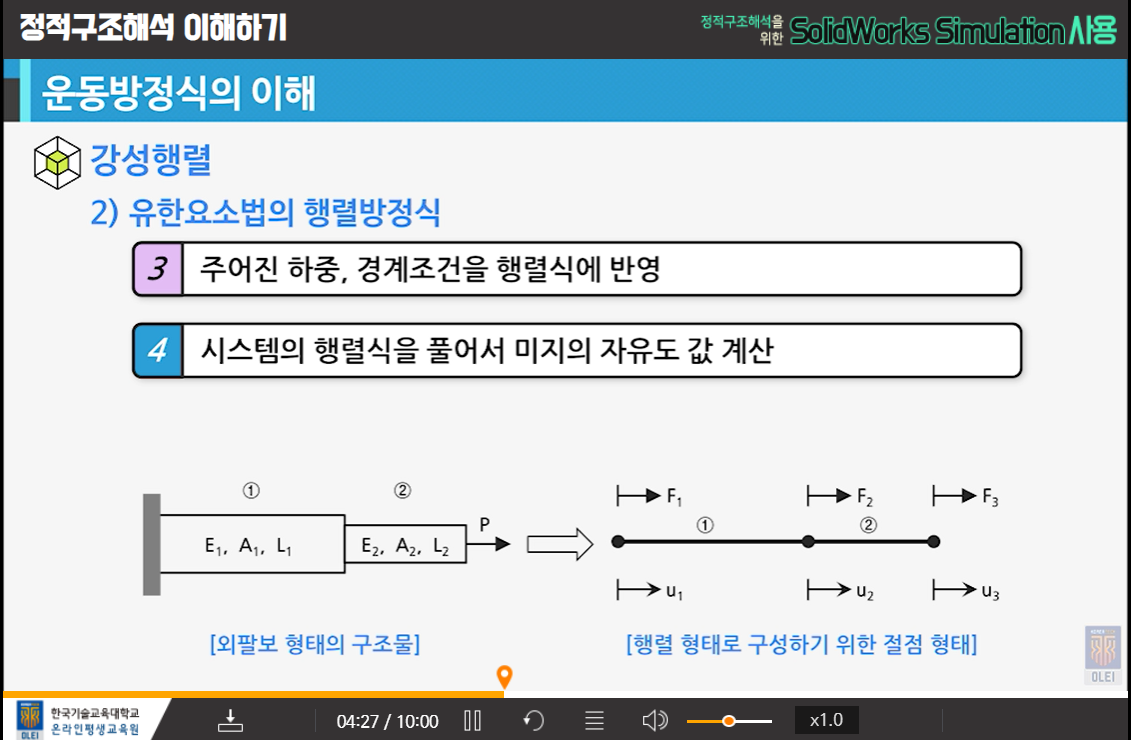
- 강성행렬
- 예정 : 운동방정식
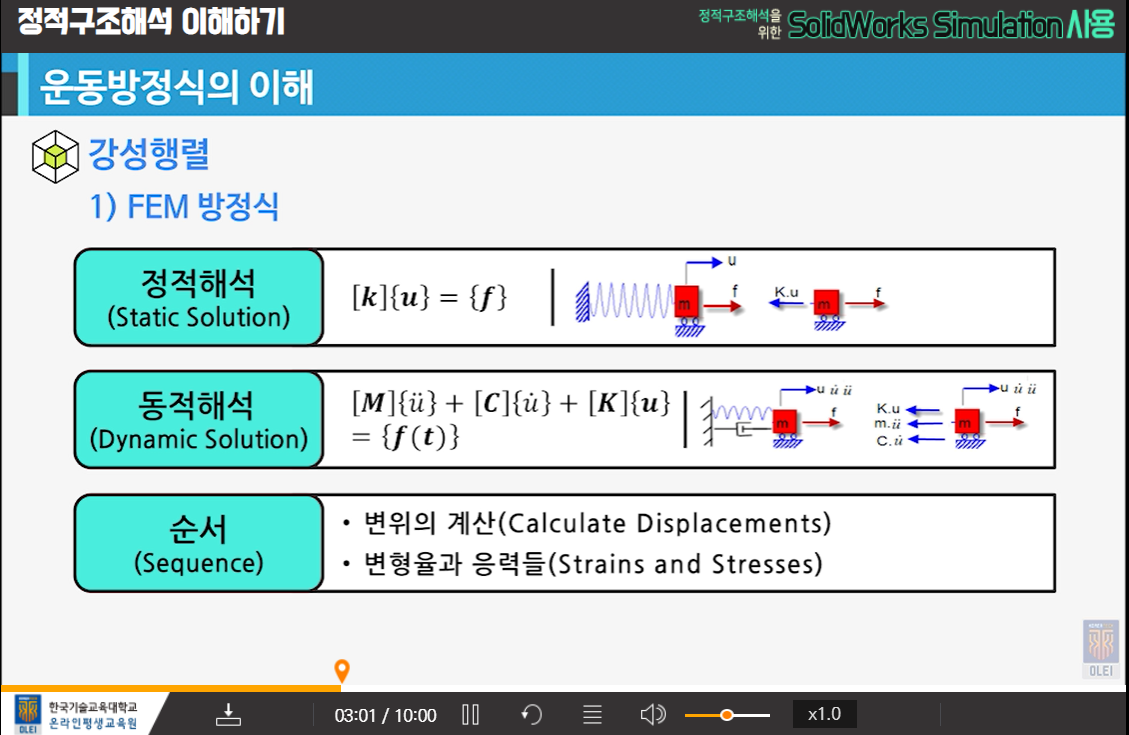
K강성 U변위 F힘


7회차 - 정적구조해석 설정하기
학습목표
- 재질 물성치의 수정방법을 설명할 수 있다.
- 핮우 및 구속 조건의 수정방법을 설명할 수 있다.
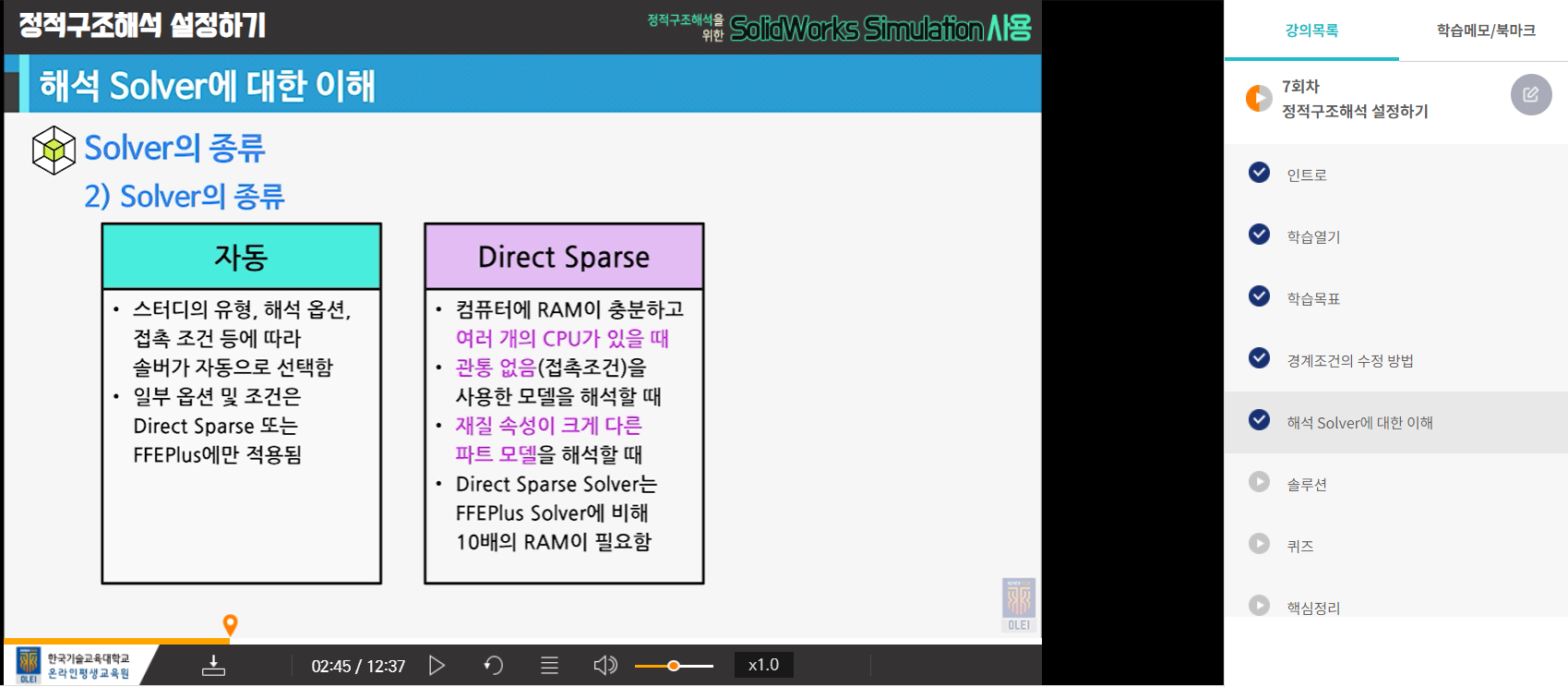
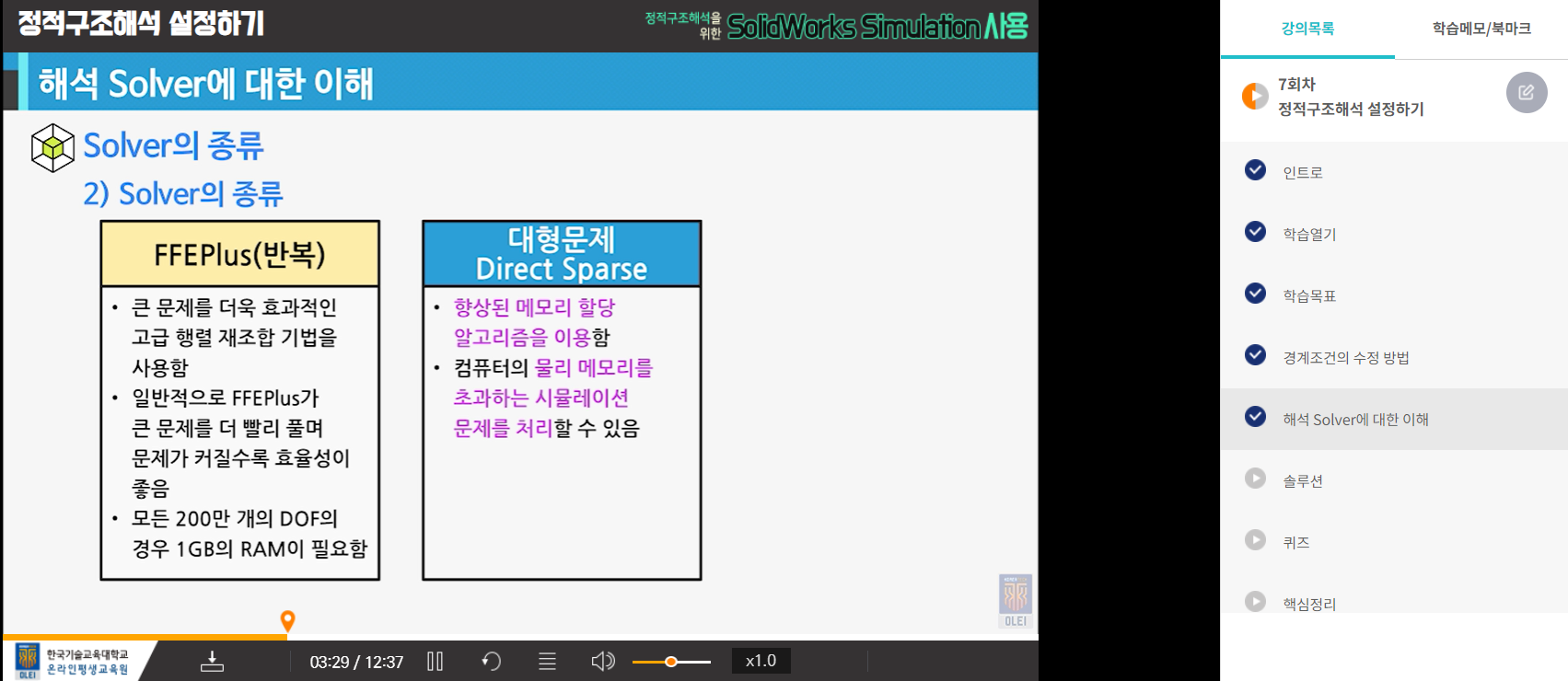
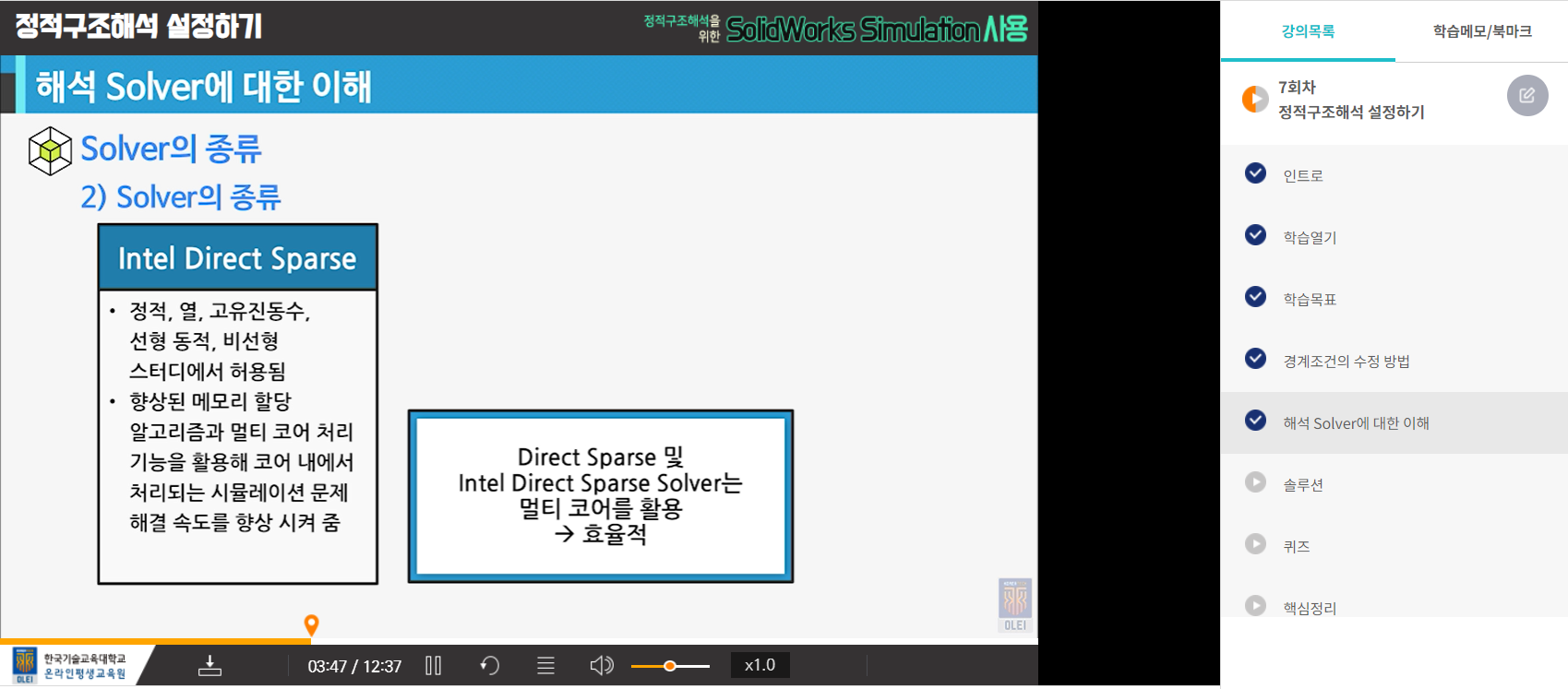
- solver의 종류에 대해 설명할 수 있다.
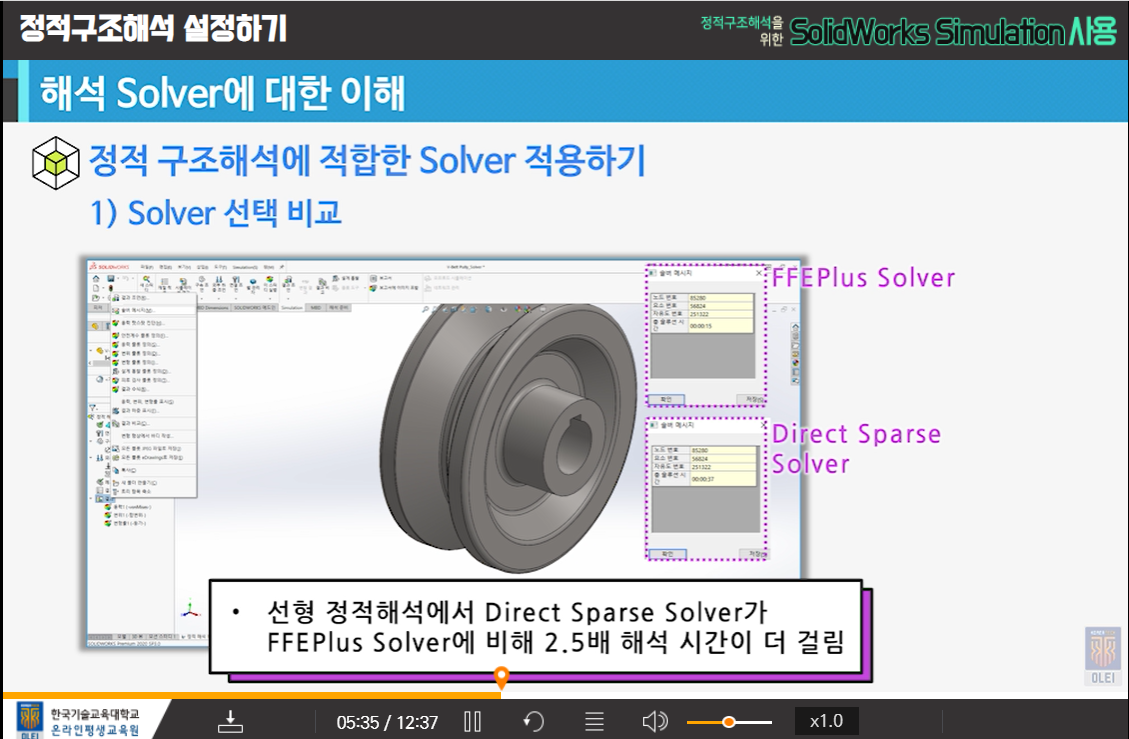
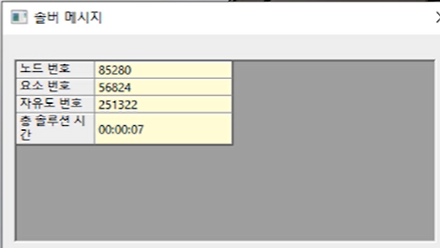
- 정적 구조해석에 적합한 solver를 적용하고 설명할 수 있다.
학습내용
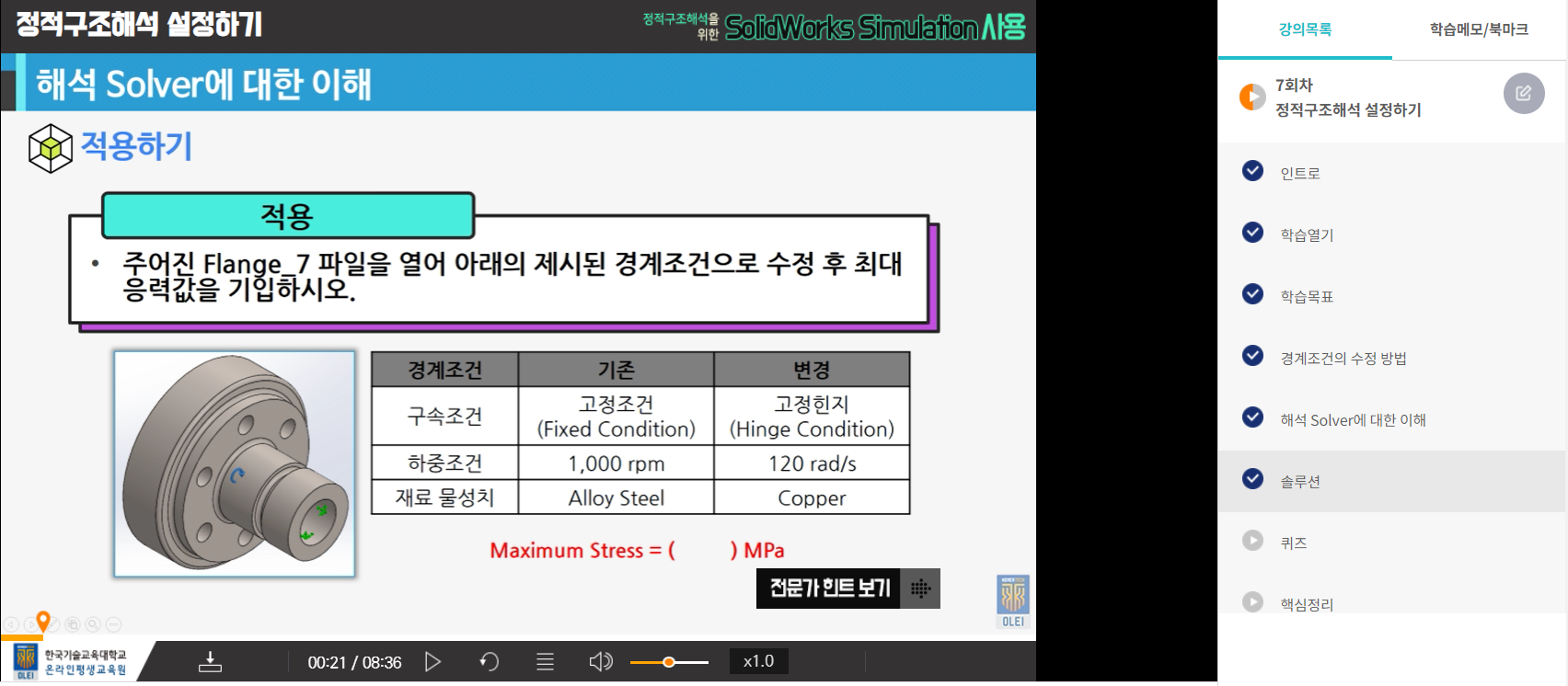
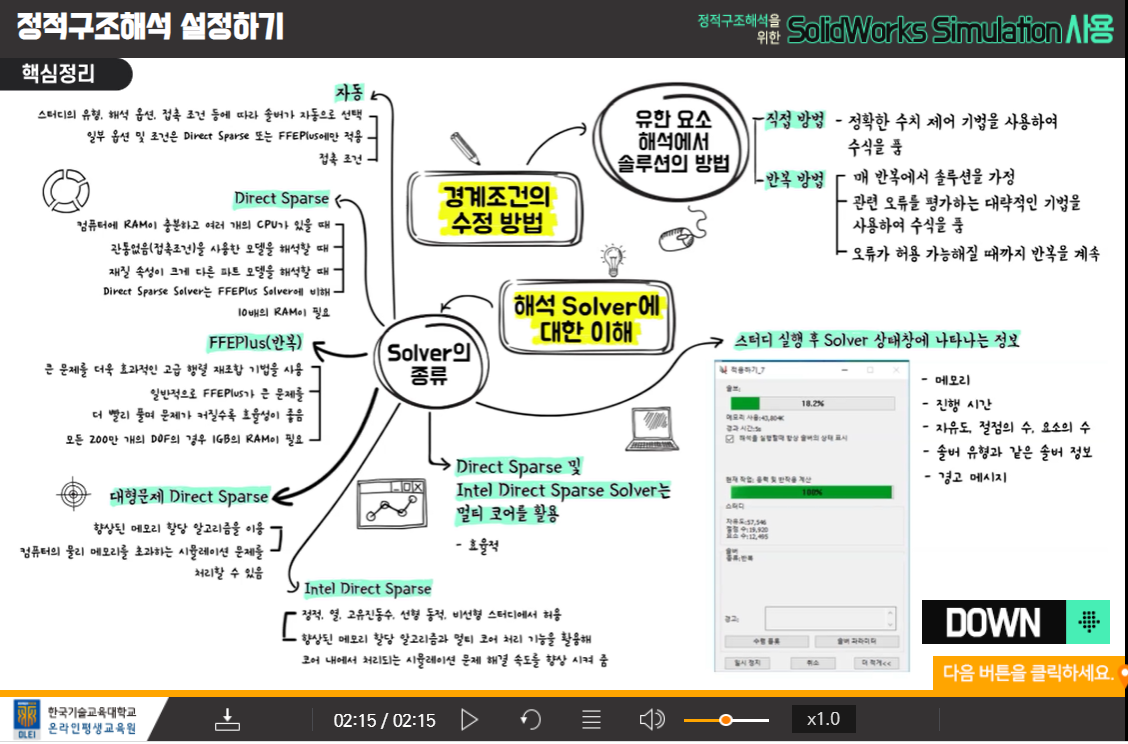
7-1. 경계조건의 수정방법
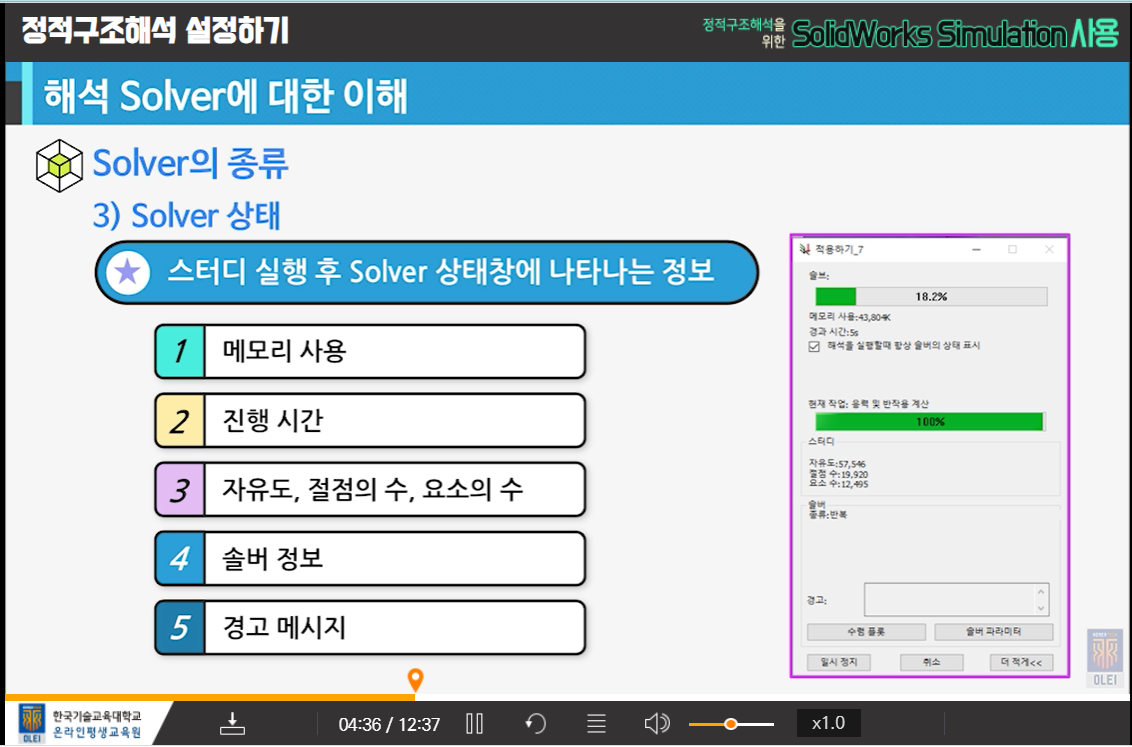
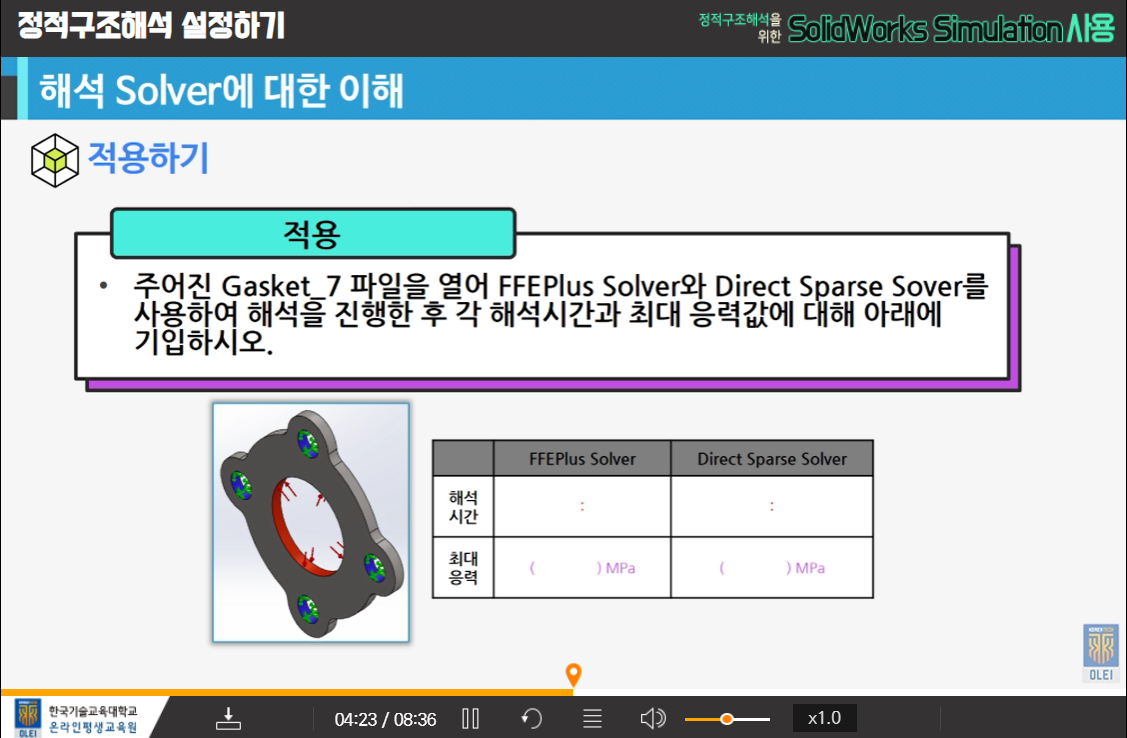
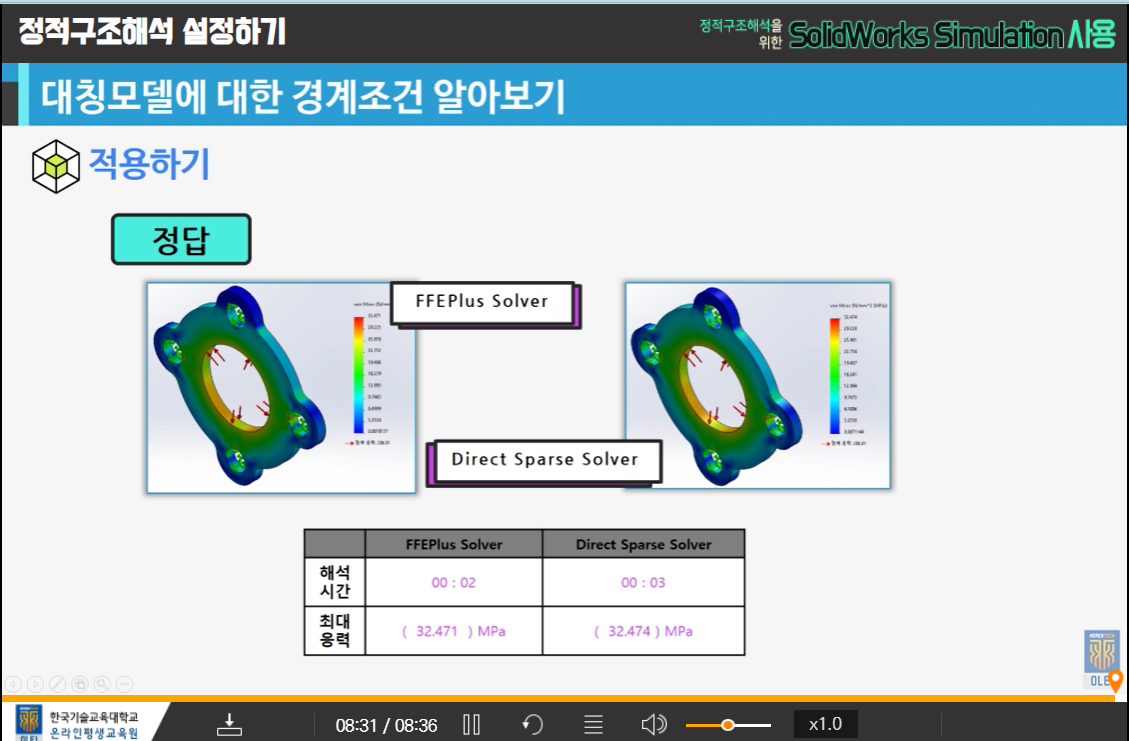
7-2. 해석 solver에 대한 이해
7-1. 경계조건의 수정방법
학습목표
- 재질 물성치의 수정방법을 설명할 수 있다.
- 하중 및 구속조건의 수정방법을 설명할 수 있다.
학습내용
- 재질물성치의 수정
- 하중 및 구속조건 수정
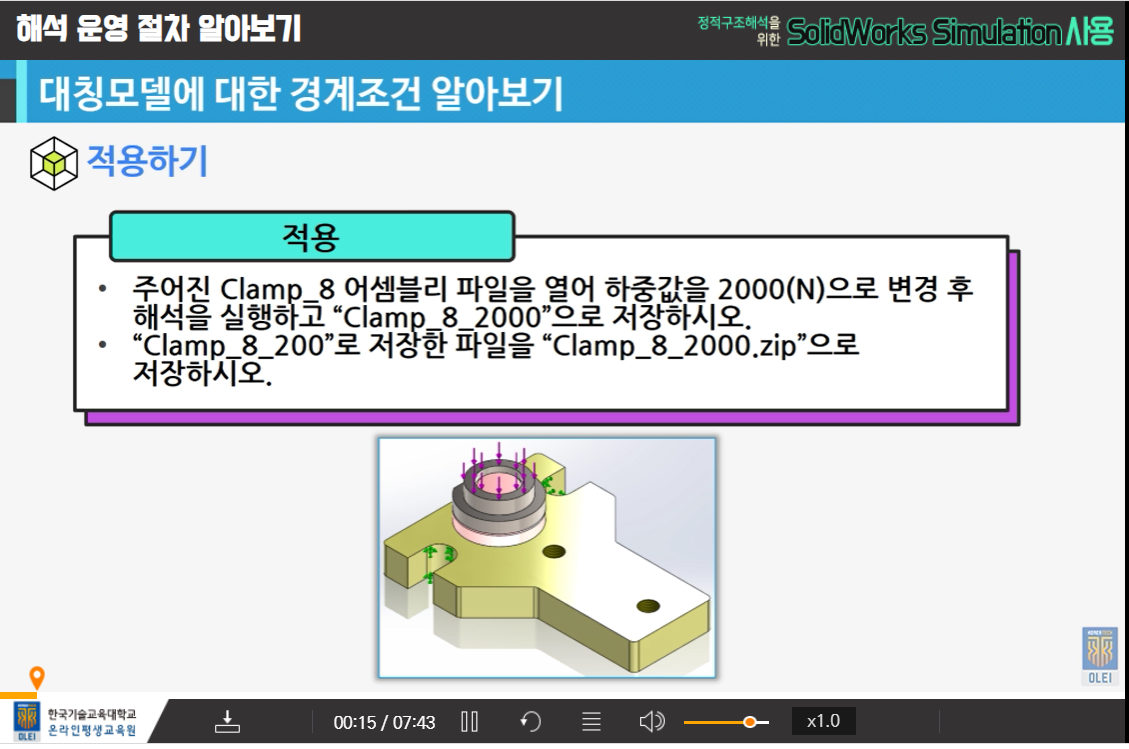
솔루션
경계조건수정방법


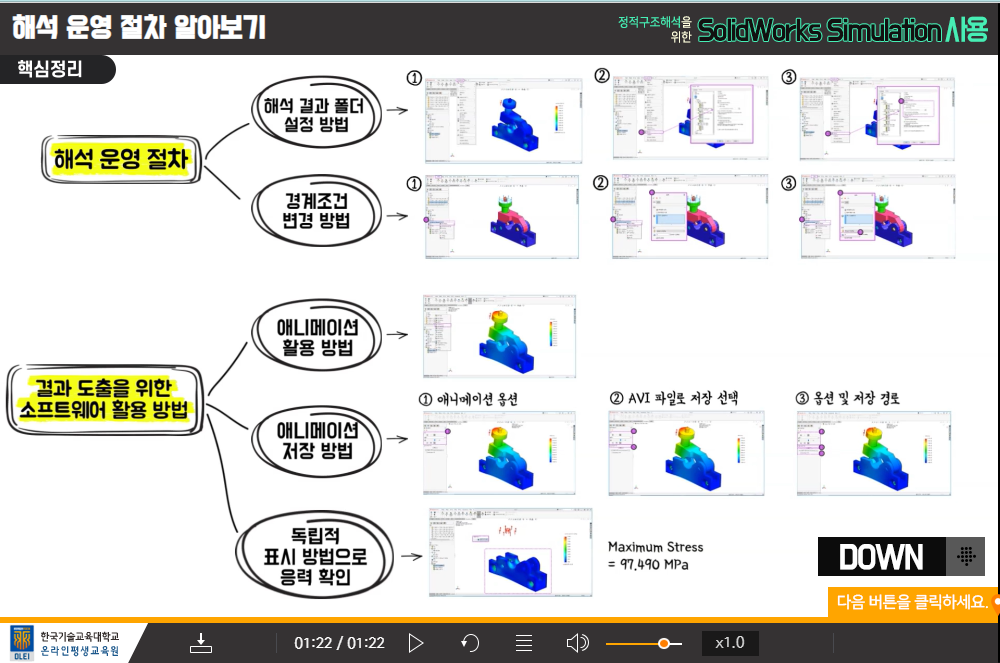
9회차
학습목표
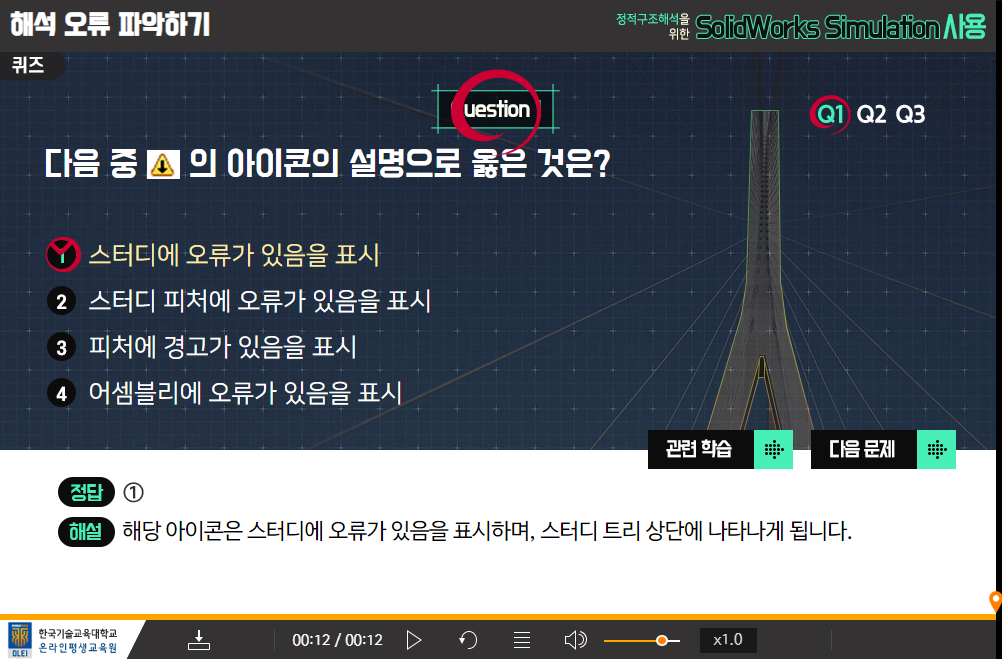
- 경계조건 오류와 메시 오류에 대해 설명할 수 있다.
- 경계조건 오류를 수정할 수 있고 메시 오류에 대한 메시 조언을 사용할 수 있다.
학습내용
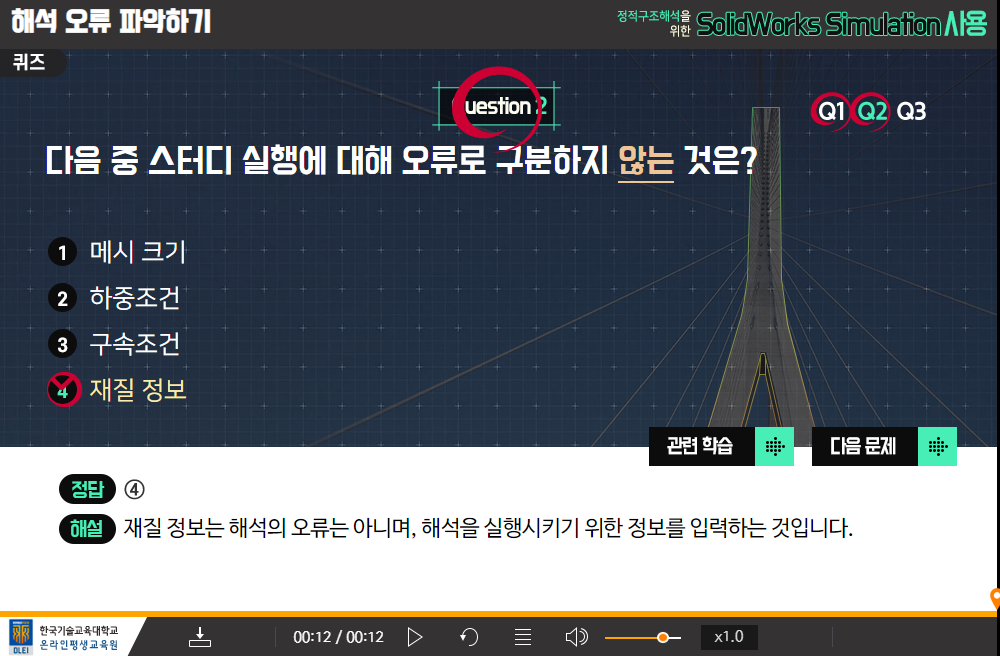
9-1. 해속 오류에 대한 검토
9-2. 오류 수정 방법

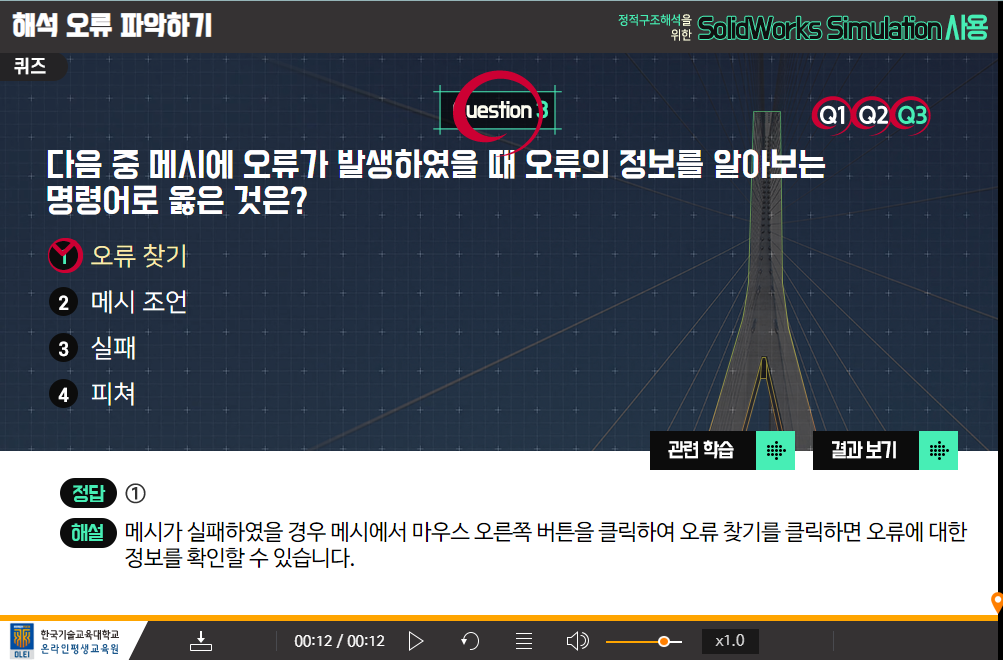
10회차 - 해석결과 확인하기
학슥목표
- 메시 컨트롤과 메시 종륭 대해 설명할 수 있다.
- 해석 결과에 대해 검토할 수 있으며 적절한 메시 요소 크기에 대해 설명할 수 있다.
학습내용
10-1. 해석 결과에 대한 신뢰성 검토
10-2. 최적 해석 결과 확인하기
10-1 해석 결과에 대한 신뢰성 검토
학습목표
- 메시 컨트롤에 대해 이해할 수 있다.
- 메시 종류에 대해 알 수 있다.
학습내용
- 메시 컨트롤에 대한 이해
- 메시 종류에 대한 이해


표준 메시 : 메시의 크기가 동일하다
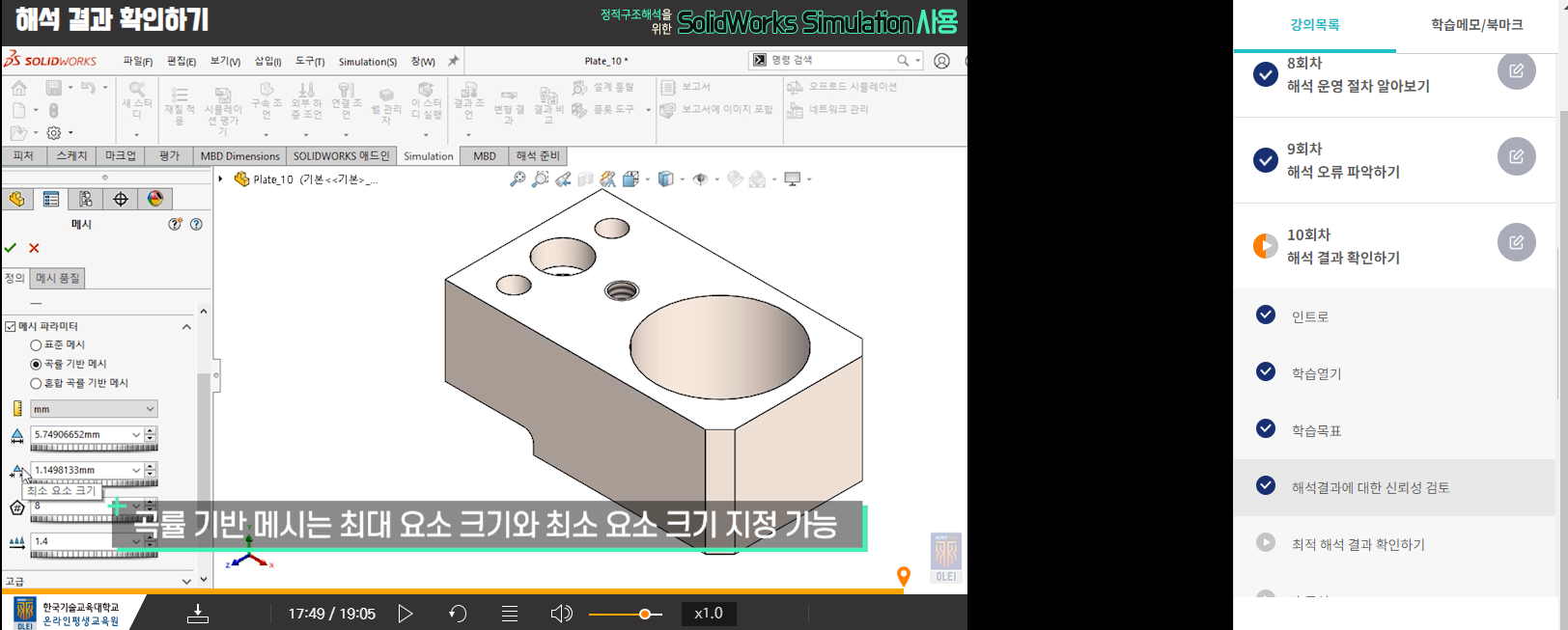
곡률 기반 메시

혼합 곡률 기반메시 : 곡률기반 메시와 별 다른 차이는 없다.
10-2 최적 해석 결과 확인하기
학습목표
- 해석 결과에 대해 검토할 수 있다.
- 적절한 메시 요소 크기에 대해 이해할 수 있다.
학습내용
- 해석 결과 검토
- 적절한 메시 요소 크기에 대한 이해
'KOREATECH' 카테고리의 다른 글
| 20221015 파이썬을 활용한 알티노로봇 (0) | 2022.10.15 |
|---|---|
| SOLIDWORKS SIMULATION TEST (0) | 2022.08.29 |
| 교육역량 개발 (0) | 2022.08.11 |
| 직업훈련교사의 사명감(전병철강사) (0) | 2022.08.11 |
| k디지털트레이닝 (0) | 2022.08.10 |



